��Ŀ����
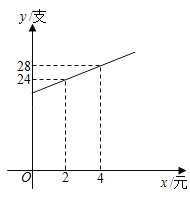
����Ŀ��С�Ӫ�ij��ε�����ijƷ�Ƴ�����Һ����֪�����Ϊ40Ԫ/֧�������η��ֽ��ۼ۶�Ϊ80Ԫ/֧ʱ��ÿ�������20֧������Ϊ��������������С���ʵ��������ۼۣ�������y��֧���뽵��x��Ԫ���Ĺ�ϵ��ͼ��ʾ��
��1������ϸ���⣬����ȫ�������
����x/Ԫ | �� | 2 | 4 | �� �� | x | �� |
����y/֧ | �� | 24 | 28 | 30 | �� �� | �� |
��2����Ҫʹ��ƽ��ÿ������������Һ������W�����ÿ֧��ҺӦ�ý��۶���Ԫ����������WΪ����Ԫ��
���𰸡���1��5��2x+20����2����ÿ֧����15Ԫʱ���������������Ϊ1250Ԫ��
��������
��1���������ô���ϵ����ȷ��һ�κ����Ľ���ʽ��Ȼ�����x��y��ֵ���y��x��ֵ���ɣ�
��2�����������г����κ�������ú�������ֵ�������𰸣�
�⣺��1����y��x�ĺ�����ϵʽΪy��kx+b��
�ɺ���ͼ����з����飺![]() ��
��
��ã�![]() ��
��
��y��x�ĺ�����ϵʽΪy��2x+20��
��y��30ʱ��30��2x+20���ã�x��5��
��ȫ�������£�
����x/Ԫ | �� | 2 | 4 | 5 | x | �� |
����y/֧ | �� | 24 | 28 | 30 | 2x+20 | �� |
�ʴ�Ϊ��5��2x+20��
��2���轵��xԪ����ÿ֧������Һ������Ϊ��80��x��40�������۵�����Ϊy��
��ÿ�����������W����80��40��x����2x+20������2��x��15��2+1250��
��a����2��0��
�൱x��15ʱ��W�����ֵΪ1250��
�൱ÿ֧����15Ԫʱ���������������Ϊ1250Ԫ��