题目内容
【题目】如图1,点![]() ,
,![]() 在反比例函数图象上,作直线
在反比例函数图象上,作直线![]() ,连接
,连接![]() 、
、![]() .
.
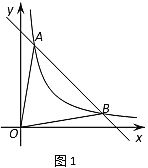
(1)求反比例函数的表达式和![]() 的值;
的值;
(2)求![]() 的面积;
的面积;
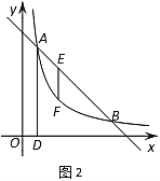
(3)如图2,![]() 是线段
是线段![]() 上一点,作
上一点,作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,交反比例函数图象于点
轴的垂线,交反比例函数图象于点![]() ,若
,若![]() ,求出点
,求出点![]() 的坐标.
的坐标.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)点
;(3)点![]() 的坐标为
的坐标为![]() 或
或![]() .
.
【解析】
(1)先根据点![]() ,利用待定系数法可求出反比例函数的解析式,再把
,利用待定系数法可求出反比例函数的解析式,再把![]() 代入解析式即可求出m的值;
代入解析式即可求出m的值;
(2)如图,先利用待定系数法求出直线AB的解析式,从而可得点M、N的坐标,再根据三角形的面积公式即可得;
(3)先设点E的坐标为![]() ,从而可得点F的坐标为
,从而可得点F的坐标为![]() ,再分别得出AD、EF的长,然后根据
,再分别得出AD、EF的长,然后根据![]() 求解即可得.
求解即可得.
(1)设反比例函数的解析式为![]()
将![]() 代入
代入![]() ,得
,得![]()
则反比例函数的解析式为![]()
把![]() 代入
代入![]() ,得
,得![]()
解得![]() ;
;
(2)设直线![]() 的解析式为
的解析式为![]()
把![]() 、
、![]() 代入得
代入得![]() ,解得
,解得![]()
则直线![]() 的解析式为
的解析式为![]()
当![]() 时,
时,![]() ,解得
,解得![]() ,则点N的坐标为
,则点N的坐标为![]()
当![]() 时,
时,![]() ,则点M的坐标为
,则点M的坐标为![]()
![]()
![]()
![]() 点A到y轴的距离等于1,点B到x轴的距离等于1
点A到y轴的距离等于1,点B到x轴的距离等于1
∴![]()
![]()
![]() ;
;
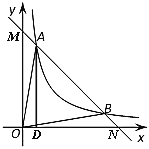
(3)由题意,可设![]() 点的坐标为
点的坐标为![]() ,则点F的坐标为
,则点F的坐标为![]() ,且
,且![]()
∴![]()
![]()
![]()
∵![]()
∴![]()
解得![]() ,
,![]()
经检验,![]() ,
,![]() 都是分式方程的根,且符合
都是分式方程的根,且符合![]() 的条件
的条件
当![]() 时,
时,![]()
当![]() 时,
时,![]()
则点![]() 的坐标为
的坐标为![]() 或
或![]() .
.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目