题目内容
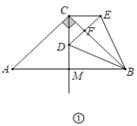
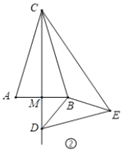
【题目】如图,等腰△ABC中,AB=AC,∠A=36°,△ABC绕点B逆时针方向旋转一定角度后到△BDE的位置,点D落在边AC上
问:(1)旋转角是几度?为什么?
(2)将AB与DE的交点记为F,除△ABC和△BDE外,图中还有几个等腰三角形?写出图中所有的等腰三角形
(3)请选择题(2)中找到的一个等腰三角形说明理由.

【答案】(1)36°,见解析;(2)5个,△BCD,△BDF,△BEF,△ADF,△ABD;(3)△BCD,见解析
【解析】
(1)根据旋转的性质,可得BD=BC,然后根据等腰三角形的性质即可求解;
(2)求得图形中的角的度数,根据等角对等边即可判断;
(3)根据等角对等边或旋转的性质判断.
解:(1)36°.
∵AB=AC,
∴∠ABC=∠C,
∵∠ABC+∠C+∠A=180°,∠A=36°,
∴∠ABC=∠C=72°.
∵BD=BC,
∴∠BDC=∠C=72°.
∴∠DBC=36°.
即旋转角为36°.
(2)图中还有5个等腰三角形,
分别是:△BCD,△BDF,△BEF,△ADF,△ABD;
(3)证:△BCD是等腰三角形.
证明:∵△ABC绕点B逆时针方向旋转一定角度后到△BDE的位置,
∴△ABC≌△BDE,
∴BD=DC,
即:△BCD是等腰三角形.

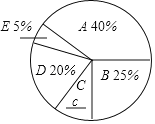
【题目】“全民阅读”活动,是中央宣传部、中央文明办和新闻出版总署贯彻落实关于建设学习型社会要求的一项重要举措.读书必须要讲究方法,只有按照一定的方法去阅读,才能取得事半功倍的效果.常用的阅读方法有:A.圈点批注法;B.摘记法;C.反思法:D.撰写读后感法;E.其他方法.某县某中学张老师为了解本校学生使用不同阅读方法读书的情况,随机抽取部分本校中学生进行了调查,通过数据的收集、整理绘制成以下不完整的统计图表,请根据图表中的信息解答下列问题:
中学生阅读方法情况统计表
阅读方法 | 频数 | |
A | 圈点批注法 | a |
B | 摘记法 | 20 |
C | 反思法 | b |
D | 撰写读后感法 | 16 |
E | 其他方法 | 4 |
(1)请你补全图表中的a,b,c数据:a= ,b= ,c= ;
(2)若该校共有中学生960名,估计该校使用“反思法”读书的学生有 人;
(3)小明从以上抽样调查所得结果估计全县6000名中学生中有1200人采用“撰写读后感法”读书,你同意小明的观点吗?请说明你的理由.
(4)该校决定从本次抽取的“其他方法”4名学生(记为甲,乙,丙,丁)中,随机选择2名成为学校阅读宣讲志愿者,请你用列表法或画树状图的方法,求恰好抽到甲和乙的概率.
【题目】某校九年级学生开展跳绳比赛活动,每班派5名学生参加,按团体总分多少排列名次,在规定时间内每人跳100个以上(含100个)为优秀.下表是甲班和乙班5名学生的比赛数据(每跳1个记1分,单位:分):
1号 | 2号 | 3号 | 4号 | 5号 | 总计 | |
甲班 | 100 | 98 | 110 | 89 | m | 500 |
乙班 | 89 | n | 95 | 119 | 97 | 500 |
经统计发现两班总分相等,此时有学生建议,可以通过考查数据中的其他信息作为参考,来确定冠军.请你回答下列问题:
(1)上表中,m=______,n=_____;
(2)若从两班参赛的这10名同学中,随机选择1人,求其成绩为优秀的概率;
(3)试从两班比赛成绩的优秀率、中位数和极差三个方面加以分析,判断冠军应该属于哪个班级?并简要说明理由.