题目内容
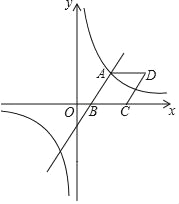
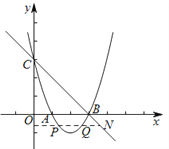
【题目】在平面直角坐标系![]() 中,抛物线y=x2-4x+3与x轴交于点A 、B(点A在点B的左侧),与y轴交于点C.
中,抛物线y=x2-4x+3与x轴交于点A 、B(点A在点B的左侧),与y轴交于点C.
(1)求直线BC的表达式;
(2)垂直于y轴的直线l与抛物线交于点![]() ,与直线BC交于点
,与直线BC交于点![]() ,若x1<x2<x3,结合函数的图象,求x1+x2+x3的取值范围.
,若x1<x2<x3,结合函数的图象,求x1+x2+x3的取值范围.
【答案】(1)y=-x+3;(2)7< x1+x2+x3<8.
【解析】试题(1)先求A、B、C的坐标,用待定系数法即可求解;
(2)由于垂直于y轴的直线l与抛物线![]() 要保证
要保证![]() ,则P、Q两点必位于x轴下方,作出二次函数与一次函数图象,找出两条临界直线,为x轴和过顶点的直线,继而求解.
,则P、Q两点必位于x轴下方,作出二次函数与一次函数图象,找出两条临界直线,为x轴和过顶点的直线,继而求解.
试题解析:(1)由抛物线![]() 与x轴交于点A,B(点A在点B的左侧),令y=0,解得x=1或x=3, ∴点A,B的坐标分别为(1,0),(3,0),
与x轴交于点A,B(点A在点B的左侧),令y=0,解得x=1或x=3, ∴点A,B的坐标分别为(1,0),(3,0),
∵抛物线![]() 与y轴交于点C,令x=0,解得y=3, ∴点C的坐标为(0,3).设直线BC的表达式为y=kx+b, ∴
与y轴交于点C,令x=0,解得y=3, ∴点C的坐标为(0,3).设直线BC的表达式为y=kx+b, ∴![]() ,解得
,解得![]() ,
,
∴直线BC的表达式为:y=-x+3.
(2).由![]() ,
,
∴抛物线的顶点坐标为(2,-1),对称轴为直线x=2,
∵![]() ,∴
,∴![]() +
+![]() =4.令y=-1,y=-x+3,x=4.
=4.令y=-1,y=-x+3,x=4.
∵![]() ,∴3<
,∴3<![]() <4, 即7<
<4, 即7<![]() <8,
<8,
∴ ![]() 的取值范围为:7<
的取值范围为:7<![]() <8.
<8.

练习册系列答案
相关题目