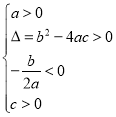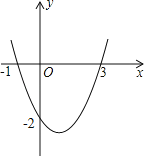题目内容
【题目】已知关于x的方程(m-1)x2-x-2=0.
(1)当m为何实数时,方程有两个不相等的实数根?
(2)若x1,x2是方程的两个根,且x![]() x2+x1x
x2+x1x![]() =-
=-![]() ,试求实数m的值.
,试求实数m的值.
【答案】(1)故m>![]() 且m≠1时,方程有两个不相等的实数根(2)m=5
且m≠1时,方程有两个不相等的实数根(2)m=5
【解析】
(1)由题意得:判别式△≥0且m-1≠0,即可得到关于m的不等式,求解即可;
(2)根据根与系数关系:求出两根之和,两根之积.由![]() =x1x2(x1+x2)=
=x1x2(x1+x2)=![]() .代入即可得到一个关于m的方程,求解即可.
.代入即可得到一个关于m的方程,求解即可.
解:(1)由题意得:△=(-1)2-4×(m-1)×(-2)=8m-7>0,
∴m>![]() .
.
又∵m-1≠0,
∴m≠1.
故m>![]() 且m≠1时,方程有两个不相等的实数根;
且m≠1时,方程有两个不相等的实数根;
(2)由题意得:x1+x2=![]() ,x1x2=-
,x1x2=-![]() .
.
∵![]() =x1x2(x1+x2)=
=x1x2(x1+x2)=![]() ,
,
∴-![]() ·
·![]() =
=![]() ,
,
∴(m-1)2=16,
∴m1=5,m2=-3.
∵m≥![]() 且m≠1,
且m≠1,
∴m=5.

练习册系列答案
相关题目
【题目】阅读下列材料:有这样一个问题:关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的且非零的实数根探究
有两个不相等的且非零的实数根探究![]() ,
,![]() ,
,![]() 满足的条件.
满足的条件.
小明根据学习函数的经验,认为可以从二次函数的角度看一元二次方程,下面是小明的探究过程:①设一元二次方程![]() 对应的二次函数为
对应的二次函数为![]() ;
;
②借助二次函数图象,可以得到相应的一元二次中![]() ,
,![]() ,
,![]() 满足的条件,列表如下:
满足的条件,列表如下:
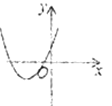
方程根的几何意义:
方程两根的情况 | 对应的二次函数的大致图象 |
|
方程有两个不相等的负实根 |
|
|
____________ |
|
|
方程有两个不相等的正实根 | ____________ | ____________ |
(1)参考小明的做法,把上述表格补充完整;
(2)若一元二次方程![]() 有一个负实根,一个正实根,且负实根大于-1,求实数
有一个负实根,一个正实根,且负实根大于-1,求实数![]() 的取值范围.
的取值范围.