题目内容
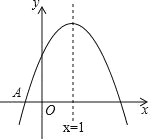
【题目】如图,直角坐标系中,抛物线y=a( x-4 )2-16(a>0)交x轴于点E,F(E在F的左边),交y轴于点C,对称轴MN交x轴于点H;直线y=![]() x+b分别交x,y轴于点A,B.
x+b分别交x,y轴于点A,B.
(1)写出该抛物线顶点D的坐标及点C的纵坐标(用含a的代数式表示).
(2)若AF=AH=OH,求证:∠CEO=∠ABO.

【答案】(1)顶点D坐标为(4,-16);点C的纵坐标为16a-16;(2)证明见解析.
【解析】
(1)根据二次函数顶点式的性质解答即可得顶点坐标,令x=0,即可得C点纵坐标;(2)根据顶点坐标及AF=AH=OH可得F、A、E点坐标,把F和A点坐标分别代入二次函数和一次函数解析式可得a、b的值,进而可求出C点坐标及OC的长,利用∠CEO和∠ABO的正切值相等即可证明∠CEO=∠ABO.
(1)∵二次函数解析式为y=a( x-4 )2-16(a>0),
∴顶点D坐标为(4,-16),
当x=0时,y=a(0-4)2-16=16a-16,
∴点C的纵坐标:16a-16.
(2)∵D(4,-16),
∴OH=4,
∵AF=AH=OH,EH=HF,
∴F(12,0),A(8,0),E(-4,0),
∴![]() ,
,![]() ,
,
![]() ,
,![]() ,
,
∴C(0,-12),OC=12,B(0,-![]() ),OB=
),OB=![]() ,
,
![]() ,
,![]() ,
,
∴∠CEO=∠ABO.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目