Question

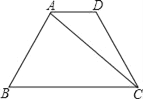
【题目】如图，在梯形ABCD中，AD∥BC，AB＝DC＝8，∠B＝60°，BC＝12，连接AC．

（1）求tan∠ACB的值；

（2）若M、N分别是AB、DC的中点，连接MN，求线段MN的长．

Answer 1

【答案】（1）；（2）8

【解析】

（1）作梯形的一条高AE，发现30°的直角三角形ABE，根据锐角三角函数求得BE，AE的长，再进一步求得CE的长，从而完成求解过程；

（2）显然MN是梯形的中位线，主要是求得上底的长即可．再作梯形的另一条高，根据全等三角形和矩形的性质求得梯形的上底．

（1）如图，作AE⊥BC于点E．

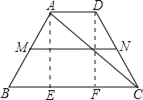
在Rt△ABE中，

BE＝ABcosB＝8×cos60°＝4，

AE＝ABsinB＝8×sin60°＝4，

∴CE＝BC﹣BE＝12﹣4＝8．

在Rt△ACE中，

tan∠ACB＝．

（2）作DF⊥BC于F，则四边形AEFD是矩形．

∴AD＝EF，DF＝AE．

∵AB＝DC，∠AEB＝∠DFC＝90°，

∴Rt△ABE≌Rt△DCF（HL）

∴CF＝BE＝4，

EF＝BC﹣BE﹣CF＝12﹣4﹣4＝4，

∴AD＝4．

又∵M、N分别是AB、DC的中点，

∴MN是梯形ABCD的中位线，

∴MN＝（AD+BC）＝（4+12）＝8．