题目内容
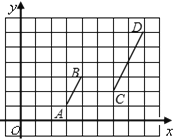
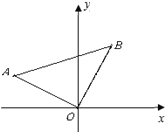
【题目】在平面直角坐标系中,△AOB的位置如图所示,已知∠AOB=90°,AO=BO,点A的坐标为(-3,1).
(1)求点B的坐标;
(2)求过A、O、B三点的抛物线的解析式;
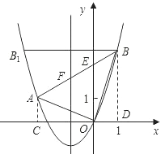
(3)设点B关于抛物线的对称轴![]() 的对称点为B1,求△AB1B的面积.
的对称点为B1,求△AB1B的面积.
【答案】(1)点B的坐标为(1,3);(2)y=![]() x2+
x2+![]() x;(3)
x;(3)![]() =
=![]() .
.
【解析】
(1)过点A作AC⊥x轴,垂足为C,作BD⊥x轴垂足为D,可证明△AOC≌△BOD,则B点的横坐标即为A点的坐标轴,B的纵坐标是A点的横坐标的绝对值,因此可求出B的坐标;(2)已知A,O的坐标,根据(1)求出的B点坐标,用待定系数法求出抛物线的解析式;(3)根据(2)的解析式可得出对称轴的解析式,根据B点坐标得出B1坐标,则BB1就是三角形的底边,B的纵坐标与A的纵坐标的查的绝对值就是△ABB1的高,因此可求出其面积.
(1)过点A作AC⊥x轴,垂足为C,作BD⊥x轴垂足为D,
则∠ACO=∠ODB=90°,
∴∠AOC+∠OAC=90°,
又∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠OAC=∠BOD,
又AO=BO,
∴△AOC≌△BOD(AAS)
∴OD=AC=1,DB=OC=3,
∴点B的坐标为(1,3)
(2)因抛物线过原点,
设所求的抛物线解析式为y=ax2+bx,
将A(-3,1),B(1,3)代入
得![]()
解得a=![]() ,b=
,b=![]()
∴所求的抛物线解析式为y=![]() x2+
x2+![]() x;
x;
(3)在y=![]() x2+
x2+![]() x中,对称轴
x中,对称轴![]()
点B1是点B关于抛物线的对称轴![]() 的对称点,
的对称点,
故B1(![]() ,3)
,3)
在△ABB1中,底边B1B=![]() ,高为2,
,高为2,
故S△ABB1=![]() .
.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目