题目内容
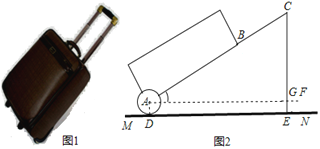
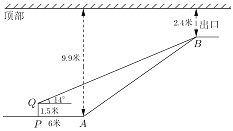
【题目】地铁10号线某站点出口横截面平面图如图所示，电梯
的两端分别距顶部9.9米和2.4米，在距电梯起点
端6米的
处，用1.5米的测角仪测得电梯终端
处的仰角为14°，求电梯的坡度与长度.（参考数据：
，
，
）
【答案】tan∠BAC
，AB＝19.5米.
【解析】
如图所示，延长PA，过B点作BC⊥PA，垂足为C，过Q点作QD∥PC，过A点作EA⊥PC，EA与QD相交于F，根据EF∥BD证得△QEF∽△QBD，根据相似比求得QD的长，进一步得到AC的长，最后求出AB的长和坡度.
如图所示，延长PA，过B点作BC⊥PA，垂足为C，过Q点作QD∥PC，过A点作EA⊥PC，EA与QD相交于F.
依题意易知，BC＝7.5，BD＝6，
EF＝APtan14°＝6×0.25＝1.5，
∵EF∥BD，∴△QEF∽△QBD，
∴
，∴QD＝24，
∴AC＝QD－PA＝18，
∴AB＝
米，
坡度为tan∠BAC＝
＝
.
新课标同步训练系列答案【题目】某水果店在两周内，将标价为10元/斤的某种水果，经过两次降价后的价格为8.1元/斤，并且两次降价的百分率相同．
（1）求该种水果每次降价的百分率；
（2）从第一次降价的第1天算起，第x天（x为整数）的售价、销量及储存和损耗费用的相关信息如表所示．已知该种水果的进价为4.1元/斤，设销售该水果第x（天）的利润为y（元），求y与x（1≤x＜15）之间的函数关系式，并求出第几天时销售利润最大？
时间x（天） | 1≤x＜9 | 9≤x＜15 | x≥15 |
售价（元/斤） | 第1次降价后的价格 | 第2次降价后的价格 | |
销量（斤） | 80﹣3x | 120﹣x | |
储存和损耗费用（元） | 40+3x | 3x2﹣64x+400 | |
（3）在（2）的条件下，若要使第15天的利润比（2）中最大利润最多少127.5元，则第15天在第14天的价格基础上最多可降多少元？
