题目内容
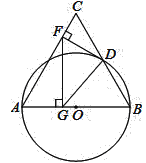
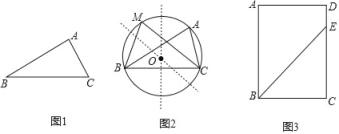
【题目】阅读:已知△ABC,用直尺与圆规,在直线BC上方的平面内作一点M(不与点A重合),使∠BMC=∠BAC(如图1).
小明利用“同弧所对的圆周角相等”这条性质解决了这个问题,下面是他的作图过程:
第一步:分别作AB、BC的中垂线(虚线部分),设交点为O;
第二步:以O为圆心,OA为半径画圆(即△ABC的外接圆)
第三步:在弦BC上方的弧上(异于A点)取一点M,连结MB、MC,则∠BMC=∠BAC.(如图2)
思考:如图2,在矩形ABCD中,BC=6,CD=10,E是CD上一点,DE=2.
(1)请利用小明上面操作所获得的经验,在矩形ABCD内部用直尺与圆规作出一点P.点P满足:∠BPC=∠BEC,且PB=PC.(要求:用直尺与圆规作出点P,保留作图痕迹.)
(2)求PC的长.
【答案】(1)详见解析;(2)![]()
【解析】
(1)作BC的垂直平分线,交BE于点O,以O为圆心,OB为半径作圆,交垂直平分线于点P,则点P为所求.
(2)先根据AD=6,CD=10,DE=2知CE=8,BE=10,从而得OB=OP=5,再由BQ=CQ=![]() BC=3得OQ=4,再根据勾股定理求解可得.
BC=3得OQ=4,再根据勾股定理求解可得.
解:(1)如图所示,点P即为所求:
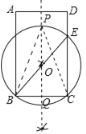
(2)∵CD=10,DE=2,
∴CE=8,
∵BC=AD=6,
∴BE=10,
则OP=OB=5,
∵BQ=CQ=![]() BC=3,
BC=3,
∴OQ=4,
则PQ=9,
∴PC=![]() =
=![]() =3
=3![]() .
.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目