Question

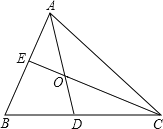
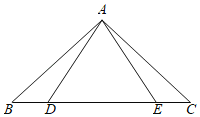
【题目】如图，在△ABC中，∠B＝∠C＝44°，点D点E分别从点B、点C同时出发，在线段BC上作等速运动，到达C点、B点后运动停止．

（1）求证：△ABE≌△ACD；

（2）若AB＝BE，求∠DAE的度数；

（3）若△ACE的外心在其内部时，求∠BDA的取值范围．

Answer 1

【答案】（1）见解析；（2）44°；（3）46°＜∠BDA＜90°

【解析】

（1）由“点D点E分别从点B、点C同时出发，在线段BC上作等速运动，”可知BD=CE，可得：BE=CD，结论易证；

（2）利用等腰三角形的判定和性质即可；

（3）根据三角形外心的位置与三角形形状的关系可得：△ACE是锐角三角形，再结合三角形内角和定理即可得到结论．

（1）证明：∵点D点E分别从点B、点C同时出发，在线段BC上作等速运动，

∴BD=CE

∴BD+DE=DE+CE，即BE=CD

∵∠B=∠C=44°

∴AC=AB

∴△ABE≌△ACD（SAS）

（2）∵AB=BE

∴∠BAE=∠AEB

∵△ABE≌△ACD

∴AD=AE

∴∠ADE=∠AEB

∴∠BAE=∠ADE，即：∠BAD+∠DAE=∠BAD+∠B

∴∠DAE=∠B=44°

（3）∵△ACE的外心在其内部

∴△ACE是锐角三角形

∴∠BDA=∠AEC＜90°

∵∠B=44°

∴∠BAD=180°﹣44°﹣∠BDA＜90°

∴∠BDA＞46°

∴46°＜∠BDA＜90°