题目内容
如图,已知 的圆心在x轴上,且经过
的圆心在x轴上,且经过 、
、 两点,抛物线
两点,抛物线 (m>0)经过A、B两点,顶点为P。
(m>0)经过A、B两点,顶点为P。

(1)求抛物线与y轴的交点D的坐标(用m的代数式表示);
(2)当m为何值时,直线PD与圆C相切?
(3)联结PB、PD、BD,当m=1时,求∠BPD的正切值。
 的圆心在x轴上,且经过
的圆心在x轴上,且经过 、
、 两点,抛物线
两点,抛物线 (m>0)经过A、B两点,顶点为P。
(m>0)经过A、B两点,顶点为P。
(1)求抛物线与y轴的交点D的坐标(用m的代数式表示);
(2)当m为何值时,直线PD与圆C相切?
(3)联结PB、PD、BD,当m=1时,求∠BPD的正切值。
(1)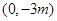 ;(2)
;(2)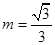 ;(3)
;(3)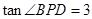
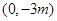 ;(2)
;(2)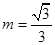 ;(3)
;(3)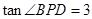
试题分析:(1)把
 、
、 代入抛物线
代入抛物线 即可得到c与m的关系,从而求得抛物线与y轴的交点D的坐标;
即可得到c与m的关系,从而求得抛物线与y轴的交点D的坐标;(2)根据切线的性质结合函数图象上点的坐标的特征即可求得结果;
(3)先把m=1代入函数关系式得到点D、P的坐标,再根据正切函数的定义即可求得结果.
(1)∵抛物线
 的图象过点
的图象过点 、
、
∴
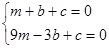 ,解得
,解得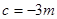
∴抛物线与y轴的交点D的坐标为
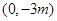 ;
;(2)∵
 经过
经过 、
、
∴点C的坐标为(-1,0),
 的半径为2
的半径为2由
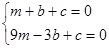 可得
可得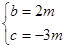
∴

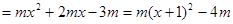
∴点P的坐标为
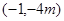
设直线PD的函数关系式为
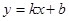
∴
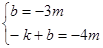 ,解得
,解得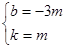
∴直线PD的函数关系式为
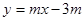
当直线PD与圆C相切
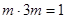 ,解得
,解得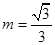 (舍负);
(舍负);(3)如图所示:
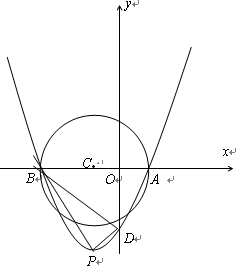
当m=1时,

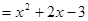
则D的坐标为(0,-3),P点坐标为(1,-4)
∴
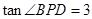 .
.点评:二次函数的综合题是初中数学的重点和难点,是中考的热点,尤其在压轴题中极为常见,要特别注意.

练习册系列答案
相关题目
 ,则称这个三角形为勾股三角形.
,则称这个三角形为勾股三角形. ,AC=
,AC= ,BC=2,BE是⊙O的直径,交AC于D.
,BC=2,BE是⊙O的直径,交AC于D. 
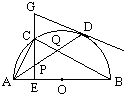

 ,OP=2,则AC的长是( )
,OP=2,则AC的长是( )



 中,∠
中,∠ 的平分线
的平分线 与△
与△ ,过
,过 ∥
∥ .
. 切线.
切线.