题目内容
【题目】如图,一次函数y=kx+b分别交x轴正半轴、y轴正半轴于点A、B,点P在边OA上运动(点P不与点O,A重合),PE⊥AB于点E,点F,P关于直线OE对称,PE:EA=3:4.若EF∥OA,且四边形OPEF的周长为6.

(1)求证:四边形OPEF为菱形;
(2)求证:OB=BE;
(3)求一次函数y=kx+b的表达式.
【答案】(1)见解析;(2)见解析;(3)y=﹣![]() x+3.
x+3.
【解析】
(1)根据全等三角形的性质以及平行线的性质得出∠EOP=∠OEP,从而得出OP=PE,进而求得OP=OF=PE=EF,即可证得四边形OPEF是菱形;
(2)求得∠BOE=∠BEO,根据等角对等边即可证得结论;
(3)根据题意求得AE=2,根据勾股定理求得AP,即可求得OA,得出A的坐标,设OB=BE=x,则AB=x+2,在Rt△AOB中,根据勾股定理列出x2+42=(2+x)2,解得x=3,得出B的坐标,然后根据待定系数法即可求得一次函数y=kx+b的表达式.
解:如图:
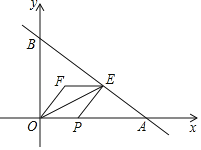
(1)∵△OPE≌△OFE,
∴OP=OF,PE=EF,∠OEF=∠OEP,
∵EF∥OA,
∴∠FEO=∠EOP,
∴∠EOP=∠OEP,
∴OP=PE,
∴OP=OF=PE=EF,
∴四边形OPEF是菱形;
(2)∵PE⊥AB,
∴∠BEP=90°,
∴∠BEP=∠BOA=90°,
∵∠EOP=∠OEP,
∴∠BOE=∠BEO,
∴OB=BE;
(3)∵四边形OPEF的周长为6,
∴OP=PE=![]()
∵PE:EA=3:4,
∴AE=2,
在Rt△PAE中,AE=2,PE=![]() ,
,
∴AP=![]() =
=![]() =
=![]() ,
,
∴AO=OP+AP=![]() +
+![]() =4,
=4,
∴A(4,0),
设OB=BE=x,则AB=x+2,
在Rt△AOB中,x2+42=(2+x)2,
解得x=3,
∴OB=3,
∴B(0,3),
∵一次函数y=kx+b分别交x轴正半轴、y轴正半轴于点A、B,
∴![]() ,解得:
,解得: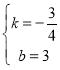 ,
,
∴一次函数y=kx+b的表达式为y=﹣![]() +3.
+3.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案