题目内容
【题目】如图,△ABC中,∠BAC=90°,AB=AC, D是△ABC内一点,∠DAC=∠DCA=15°,则∠BDA=______.
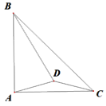
【答案】75°
【解析】
以AD为边,在△ADB中作等边三角形ADE,连接BE.可证得△EAB≌△DAC,再证△BEA≌△BED,得到BA=BD,利用等边对等角即可得结论.
如图,以AD为边,在△ADB中作等边三角形ADE,连接BE.
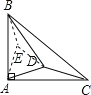
∵∠BAE=90°-60°-15°=15°,
∴∠BAE=∠CAD=15°,
在△EAB和△DAC中,
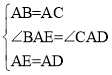
∴△EAB≌△DAC(SAS),
∴∠BEA=∠CDA=180°-15°-15°=150°,
∴∠BED=360°-∠BEA-60°=150°,即∠BEA=∠BED;
在△BEA和△BED中,
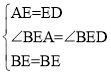
∴△BEA≌△BED(SAS),
∴BA=BD.
∴∠BDA=∠BAD=90°-∠DAC=75°
故答案为:75°.

练习册系列答案
 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目