Question

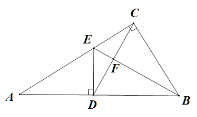
【题目】在△ABC中，AB=13，AC=5，BC边上的中线AD=6，点E在AD的延长线上，且AD=DE．

（1）试判断△ABE的形状并说明理由；

（2）求△ABC的面积．

Answer 1

【答案】（1）△ABE是直角三角形；证明见解析；（2）30

【解析】

（1）证明△ACD≌△EBD，得到BE=AC=5，再由AE=12，AB=13，得到∠E=90°，从而得到结论；

（2）由△ACD≌△EBD ，得到S△ABC=S△ABE，从而得到结论．

（1）∵AD为BC边上的中线，∴BD=CD．

在△ACD与△EBD中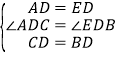，∵，∴△ACD≌△EBD，∴BE=AC=5．

∵AD=DE=6，∴AE=12．

∵AE2+BE2=52+122=169，AB2=132=169，∴AE2+BE2= AB2，∴∠E=90°，∴△ABE是直角三角形．

（2）∵△ACD≌△EBD ，∴S△ABC=S△ABE=×EA×BE=×12×5 =30．