题目内容
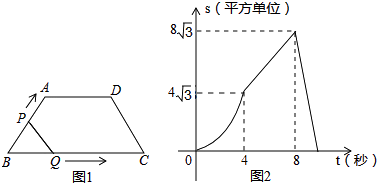
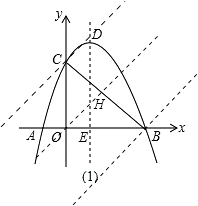
【题目】如图(1),在平面直角坐标系xOy中,抛物线y=ax2+bx+c(a≠0)与x轴交于A(﹣1,0),B(3,0),与y轴交于C(0,3),顶点为D(1,4),对称轴为DE.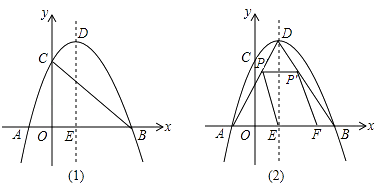
(1)抛物线的解析式是;
(2)如图(2),点P是AD上一个动点,P′是P关于DE的对称点,连接PE,过P′作P′F∥PE交x轴于F.设S四边形EPP′F=y,EF=x,求y关于x的函数关系式,并求y的最大值;
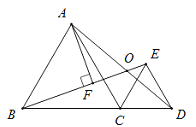
(3)在(1)中的抛物线上是否存在点Q,使△BCQ成为以BC为直角边的直角三角形?若存在,求出Q的坐标;若不存在.请说明理由.
【答案】
(1)y=﹣x2+2x+3
(2)
解:令PP′交DE于G,
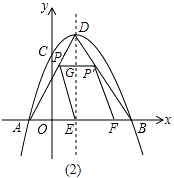
∵PP′∥AF,PE∥FP′,
∴四边形FEP′P是平行四边形,
∴PP′=EF,
∴△DPP′∽△DAB,
∴ ![]() ,
,
又∵A(﹣1,0)、B(3,0)、D(1,4),EF=x,
∴AB=4,DE=4,PP′=x,
∴ ![]()
∴GE=4﹣x,
又∵S四边形EPP'F=EFGE,
∴y=x(4﹣x)
∴y=x(4﹣x)=﹣(x﹣2)2+4,x=2时,y的最大值是4
(3)
解:假设存在满足条件的点Q(x,y),
作OH⊥BC于H,
∵Rt△BCQ中BC是直角边,
∴Rt△BCQ的另一直角边与OH平行.
又∵OC=OB,CO⊥OB,OB=3,OC=3,
∴Rt△BCQ的另一直角边所在的直线可以由直线OH向上或向右平移3个单位得到(如图).
由已知得直线OH的解析式是y=x,
∴Rt△BCQ的另一直角边所在的直线解析式是:y=x+3或 y=x﹣3
点Q为直线y=x+3和抛物线交点,
则 ![]() ,
,
解得:x=1,
∴y=4;
②点Q为直线y=x﹣3和抛物线交点,
则 ![]() ,
,
解得:x=﹣2,
∴y=﹣5,
∴存在满足条件的点Q的坐标是:(1,4)和(﹣2,﹣5)
【解析】解:(1)∵抛物线y=ax2+bx+c(a≠0)经过点C,
则c=3,
∵抛物线经过A,B两点,∴ ![]()
解得:a=﹣1,b=2,
所以答案是 y=﹣x2+2x+3;
【考点精析】利用二次函数的性质对题目进行判断即可得到答案,需要熟知增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案