Question

【题目】如图1，平面直角坐标系中，矩形ABCD关于y轴对称，点A，D在x轴上，BC交y轴于点F，E是OF的中点，抛物线y=ax2+bx+c经过B，E，C三点，已知点B（﹣2，﹣2），解答下列问题：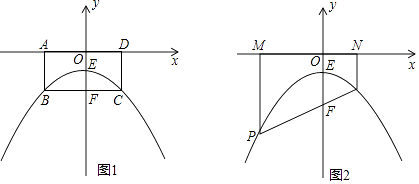

（1）填空：a= ， b= ， c= ．
（2）如图2，这P是上述抛物线上一点，连接PF并延长交抛物线于另外一点Q，PM⊥x轴于M，QN⊥x轴于N．
①求证：PM+QN=PQ；
②若PQ=m，S四边形PMNQ= m2 ， 求直线PQ对应的一次函数的解析式．

Answer 1

【答案】
（1）﹣ ；0；﹣1
（2）

解：①设点P（x，﹣ x2﹣1），则PM=|﹣ x2﹣1|= x2+1，

∵点F（0，﹣2），

∴PF=

=

=

=

= x2+1，

∴PM=PF，

同理可得QN=QF，

则PM+QN=PF+QF=PQ；

②由①知，PM+PN=PQ=m，

∵S四边形PMNQ= m2，即 （PM+PN）×MN= m2，

∴MN= m，

如图，过点P作PH⊥NQ的延长线于点H，

则PH=MN= m，

∴QH= = = ，

∴kPQ= = = ，

又∵PQ过点F（0，﹣2），

∴直线PQ对应的一次函数的解析式为y﹣（﹣2）= （x﹣0），即y= x﹣2

【解析】解：（1）由题意知点E（0，﹣1），
设抛物线解析式为y=ax2﹣1，
将点B（﹣2，﹣2）代入，得：﹣2=4a﹣1，
解得：a=﹣ ，
∴y=﹣ x2﹣1，
则a=﹣ ，b=0，c=﹣1，
所以答案是：﹣ ，0，﹣1；