题目内容
【题目】如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于点D,且∠D=2∠CAD. 
(1)求∠D的度数;
(2)若CD=2,求BD的长.
【答案】
(1)解:∵OA=OC,
∴∠A=∠ACO,
∴∠COD=∠A+∠ACO=2∠A,
∵∠D=2∠A,
∴∠D=∠COD,
∵PD切⊙O于C,
∴∠OCD=90°,
∴∠D=∠COD=45°;
(2)解:∵∠D=∠COD,CD=2,
∴OC=OB=CD=2,
在Rt△OCD中,由勾股定理得:22+22=(2+BD)2,
解得:BD=2 ![]() ﹣2.
﹣2.
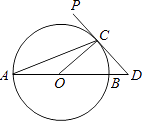
【解析】(1)根据等腰三角形性质和三角形外角性质求出∠COD=2∠A,求出∠D=∠COD,根据切线性质求出∠OCD=90°,即可求出答案;(2)求出OC=CD=2,根据勾股定理求出BD即可.

练习册系列答案
相关题目








