��Ŀ����
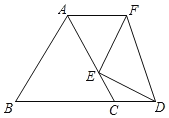
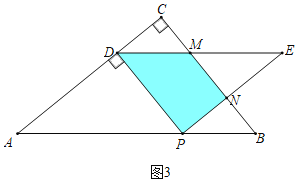
����Ŀ����ͼ����Rt��ABC�У���C��90����AC��8��BC��6������P�ӵ�A��������AB��ÿ��5����λ���ȵ��ٶ����յ�B�˶�������P�����A�غ�ʱ������P��PD��AC�ڵ�D��PE��AC������D��DE��AB��DE��PE���ڵ�E�����P���˶�ʱ��Ϊt�룮
��1���߶�AD�ij�Ϊ�� �������ú�t�Ĵ���ʽ��ʾ����
��2������E����BC����ʱ����t��ֵ��
��3������DPE����ABC�ص�����ͼ�ε����ΪS����S��t֮��ĺ�����ϵʽ��
��4�����߶�PE���е�ΪQ������Q������ABCһ�ߴ�ֱƽ������ʱ��ֱ��д��t��ֵ��

���𰸡���1��4t����2��t��ֵΪ1����3��S��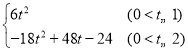 ����4��t��ֵΪ
����4��t��ֵΪ![]() ��
��![]() ��1��
��1��
��������
��1����ֱ�����������AB������cosA=![]() =
=![]() ��⼴�ɣ�
��⼴�ɣ�
��2������֤���ı���APED��ƽ���ı��Σ���![]() =
=![]() ���������̼��ɽ�����⣮
���������̼��ɽ�����⣮
��3�����������Σ�����ͼ1�У���0��t��1ʱ������ͼ3�У���1��t��2ʱ���ֱ���⼴�ɣ�
��4�����������Σ�����ͼ4-1�У�����Q�����߶�AC�Ĵ�ֱƽ����MN��ʱ������ͼ4-2�У�����Q�����߶�AB�Ĵ�ֱƽ����MN��ʱ������ͼ4-3�У�����Q�����߶�BC�Ĵ�ֱƽ������ʱ���ֱ���⼴�ɣ�
�⣺��1����ͼ1�У�
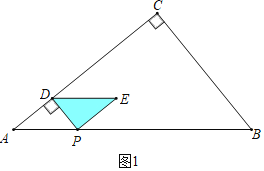
��Rt��ACB�У��ߡ�C��90����AC��8��BC��6��
��AB��![]() ��
��![]() ��10��
��10��
��PD��AC��
��cosA��![]() =
=![]() ��
��
��![]() ��
��![]() ��
��
��AD��4t��
�ʴ�Ϊ4t��
��2����ͼ2�У�����E����BC��ʱ��
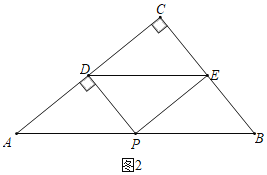
��DE��AB��PE��AD��
���ı���APED��ƽ���ı��Σ�
��DE��AP��5t��AD��PE��4t��
��![]() =
=![]() ��
��
��![]() ��
��![]()
���t��1��
�൱��E����BC����ʱ��t��ֵΪ1��
��3������ͼ1�У���0��t��1ʱ���ص���������PDE��
��PE��AD��
���DPE����ADP��90����
��DE��5t��PE��4t��
��PD��3t��
��S��![]() PDPE��
PDPE��![]() ��3t��4t��6t2��
��3t��4t��6t2��
����ͼ3�У���1��t��2ʱ��S��![]() ��MN+PD��PN��
��MN+PD��PN��![]() [3t+3t��
[3t+3t��![]() ��10��5t��]
��10��5t��]![]() ��10��5t������18t2+48t��24��
��10��5t������18t2+48t��24��
����������S�� ��
��
��4������ͼ4��1�У�����Q�����߶�AC�Ĵ�ֱƽ����MN��ʱ��
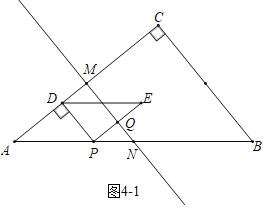
�����⣺![]() ���ɵ�
���ɵ�![]() �����t��
�����t��![]() ��
��
����ͼ4��2�У�����Q�����߶�AB�Ĵ�ֱƽ����MN��ʱ��
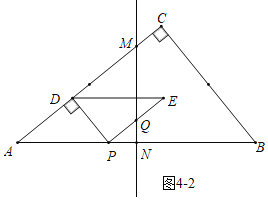
�����⣺![]() ���ɵ�
���ɵ�![]() �����t��
�����t��![]()
����ͼ4��3�У�����Q�����߶�BC�Ĵ�ֱƽ������ʱ��AP��PB����ʱt��1��
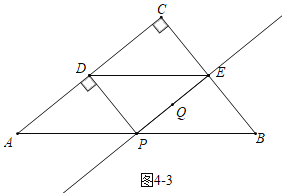
��������������������t��ֵΪ![]() ��
��![]() ��1��
��1��