题目内容
【题目】如图，某高楼顶部有一信号发射塔，小凡在矩形建筑物ABCD的A、C两点处测得塔顶F的仰角分别为α和β，AD=18m，CD=78m．
（1）用α和β的三角函数表示CE；
（2）当α=30°、β=60°时，求EF（结果精确到1m）．
（参考数据： 
≈1.414， 
≈1.732）
【答案】
（1）
解：延长AD交FE于G，
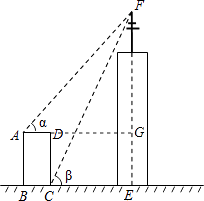
设CE=x，则DG=x，
在Rt△AFG中，tanα= 
，
∴GF=AGtanα=（x+18）tanα，
在Rt△FCE中，tanβ= 
，
FE=xtanβ，
∵FE=FG+EG，
∴xtanβ=（x+18）tanα+78，
解得，x= 
，
即CE= ；
（2）
解：FE=xtanβ
= ×tanβ
= 
= 
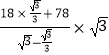
=9 
+117
≈133（m）
【解析】（1）延长AD交FE于G，设CE=x，根据正切的概念用含x的代数式表示GF、EF，根据题意列出方程，解方程即可；（2）把已知数据代入（1）中的关系式，根据特殊角的三角函数值和二次根式的运算法则计算即可．
【考点精析】解答此题的关键在于理解关于仰角俯角问题的相关知识，掌握仰角：视线在水平线上方的角；俯角：视线在水平线下方的角．
练习册系列答案
名校课堂系列答案
相关题目
【题目】一辆汽车在公路上匀速行驶，下表记录的是汽车在加满油后油箱内余油量y（升）与行驶时间x（时）之间的关系：
行驶时间x（时） | 0 | 1 | 2 | 2.5 |
余油量y（升） | 100 | 80 | 60 | 50 |
（1）小明分析上表中所给的数据发现x，y成一次函数关系，试求出它们之间的函数表达式（不要求写出自变量的取值范围）；
（2）求汽车行驶4.2小时后，油箱内余油多少升？
