题目内容
【题目】如图,AB是⊙O的直径,C是⊙O上一点,CD⊥AB于D,且AB=8,DB=2. 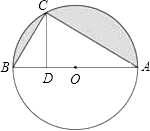
(1)求证:△ABC∽△ACD;
(2)求图中阴影部分的面积.
【答案】
(1)证明:∵AB是直径,
∴∠ACB=90°,
∵CD⊥AB,
∴∠ADC=90°,
∴∠ADC=∠ACB,∠B+∠BAC=90°,∠DCA+∠CAB=90°,
∴∠B=∠ACD,
∴△ABC∽△ACD
(2)解:∵△ABC∽△ACD,
∴ ![]() =
= ![]() ,
,
∴AC2=ADAB=6×8=48,
∴CD= ![]() =
= ![]() =2
=2 ![]() ,
,
∴S△ABC= ![]() ABCD=
ABCD= ![]() ×
× ![]() =8
=8 ![]() ,
,
∴S阴=S半圆﹣S△ABC=8 ![]() .
.

【解析】(1)根据两角对应相等的两个三角形相似即可证明.(2)先利用△ABC∽△ACD,得AC2=ADAB=48,再利用勾股定理求出CD,根据S阴=S半圆﹣S△ABC即可解决问题.
【考点精析】利用扇形面积计算公式和相似三角形的判定与性质对题目进行判断即可得到答案,需要熟知在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2);相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

 优等生题库系列答案
优等生题库系列答案【题目】2018年6月上海语文把小学教材中“外婆”改成“姥姥一事,引起社会的广泛关注和讨论,明德集团某校文学社就此召开了一次研讨会,为了传承中国传统文化,并组织了一次全体学生“汉字听写”大赛,每位学生听写汉字39个,随机抽取了部分学生的听写结果作为样本进行整理,绘制成如下的统计图表:

组别 | 正确字数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
根据以上信息完成下列问题:
(1)求统计表中的m,n,并补全条形统计图;
(2)扇形统计图中“C组“所对应的圆心角的度数是多少;
(3)已知该校共有600名学生,如果听写正确的字的个数不少于24个定为合格,请你估计该校本次听写比赛合格的学生人数.