题目内容
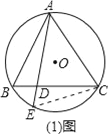
【题目】如图,△ABC内接于⊙O,且AB=AC,
(1)⊙O的弦AE交于BC于D.求证:ABAC=ADAE;
(2)在(1)的条件下当弦AE的延长线与BC的延长线相交于点D时,上述结论是否还成立?若成立,请给予证明.若不成立,请说明理由.
(3)已知⊙O 的半径2,∠ACB=40°,求BA的长.(sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,结果精确到0.1)
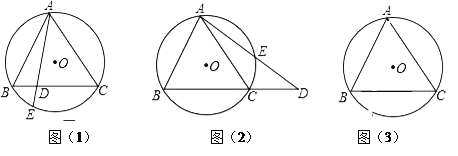
【答案】(1)证明见解析;(2)上述结论仍成立,理由见解析;(3)AB≈2.6.
【解析】(1)证明:连接CE,
∵AB=AC,
∴![]() ,
,
∴∠AEC=∠ACD;
又∵∠EAC=∠DAC,
∴△AEC∽△ACD,
∴![]() ,即AC2=ADAE;
,即AC2=ADAE;
又∵AB=AC,
∴ABAC=ADAE.
(2)答:上述结论仍成立.
证明:连接BE,
∵AB=AC,
∴![]() ,
,
∴∠AEB=∠ABD;
又∵∠EAB=∠DAB
∴△AEB∽△ABD,
∴![]() ,即AB2=ADAE.
,即AB2=ADAE.
又∵AB=AC,
∴ABAC=ADAE.
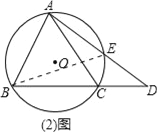
(3)解:过A作⊙O的直径AM,连接BM.
∴∠AMB=90°,
∵∠AMB=∠ACB=40°,
在Rt△ABD中,AM=4,
∵sin∠AMB =0.64,
∴AB=4sin40°=4×0.64≈2.6.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目