题目内容
【题目】如图,四边形ABCD是正方形,点E是平面内异于点A的任意一点,以线段AE为边作正方形AEFG,连接EB,GD.
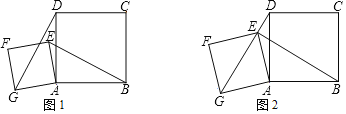
(1)如图1,求证EB=GD;
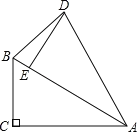
(2)如图2,若点E在线段DG上,AB=5,AG=3![]() ,求BE的长.
,求BE的长.
【答案】(1)见解析;(2)BE=7.
【解析】
(1)根据正方形的性质得出条件证明△AGD≌△AEB,即可证明EB=GD.
(2)作AH⊥DG,根据勾股定理算出EG,再推出AH,再由勾股定理求出DH,即可求出BE.
(1)证明:∵四边形ABCD和四边形BEFG都是正方形,
∴AB=AD,AG=AE,∠BAD=∠GAE=90°,
∴∠BAE=∠DAG,
在△AGD和△AEB中

∴△AGD≌△AEB(SAS),
∴EB=GD;
(2)解:作AH⊥DG于H,

∵四边形ABCD和四边形BEFG都是正方形,
∴AD=AB=5,AE=AG=3![]() .
.
∴由勾股定理得:EG=![]() =6,
=6,
AH=GH=![]() EG=3(直角三角形斜边上的中线等于斜边的一半),
EG=3(直角三角形斜边上的中线等于斜边的一半),
∴DH=![]() =4,
=4,
∴BE=DG=DH+GH=3+4=7.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目