Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņń≥—Ý÷≥Ļęňĺ◊ľĪł‘ňňÕ152Ōš–°ŃķŌļĶĹA°ĘBŃĹĶōŌķ Ř£¨ł√Ňķ–°ŃķŌļł’ļ√ń‹”√īů–°Ľű≥Ķ15Ńĺ“Ľīő‘ňÕÍ£¨“—÷™īůĽű≥Ķ√ŅŃĺń‹◊į12Ōš£¨–°Ľű≥Ķ√ŅŃĺń‹◊į8Ōš£¨∆š÷–√ŅŃĺīůĽű≥Ķ‘ňÕýA°ĘBŃĹĶōĶń‘ň∑—∑÷Īūő™800‘™ļÕ900‘™£Ľ√ŅŃĺ–°Ľű≥Ķ‘ňÕýA°ĘBŃĹĶōĶń‘ň∑—∑÷Īūő™400‘™ļÕ600‘™£ģ
£®1£©«ů’‚15Ńĺ≥Ķ÷–īů–°Ľű≥Ķłų”–∂ŗ…ŔŃĺ£Ņ
£®2£©Ō÷į≤ŇŇ∆š÷–10ŃĺĽű≥Ķ«įÕýAĶō£¨∆š”ŗĽű≥Ķ«įÕýBĶō£¨…Ť«įÕýAĶōĶńīůĽű≥Ķő™mŃĺ£¨«įÕýA°ĘBŃĹĶō◊‹∑—”√ő™y‘™£¨ ‘«ů≥Ųy”ŽmĶńļĮ żĹ‚őŲ Ĺ£¨≤Ę–ī≥ŲmĶń»°÷Ķ∑∂őߣĽ
£®3£©‘ŕ£®2£©ĶńŐűľĢŌ¬£¨»Ű‘ňÕýBĶōĶń∑—”√≤ĽłŖ”ŕAĶō∑—”√Ķń“ĽįŽ£¨«ůīň ĪĶń◊ÓĶÕ◊‹‘ň∑—£ģ
°ĺīūįł°Ņ£®1£©īůĽű≥Ķ8Ńĺ£¨–°Ľű≥Ķ7Ńĺ£Ľ£®2£©y=100x+9400£ģ£®3°‹x°‹8£©£Ľ£®3£©īň ĪĶń◊ÓĶÕ◊‹‘ň∑— «10100‘™£ģ
°ĺĹ‚őŲ°Ņ
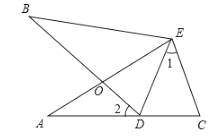
£®1£©…ŤīůĽű≥Ķ”√xŃĺ£¨–°Ľű≥Ķ”√yŃĺ£¨łýĺ›īů°Ę–°ŃĹ÷÷Ľű≥ĶĻ≤15Ńĺ£¨‘ň š152Ōš–°ŃķŌļ£¨Ń–∑Ĺ≥Ő◊ť«ůĹ‚£Ľ
£®2£©…Ť«įÕýAĶōĶńīůĽű≥Ķő™xŃĺ£¨‘Ú«įÕýBĶōĶńīůĽű≥Ķő™£®8-x£©Ńĺ£¨«įÕýAĶōĶń–°Ľű≥Ķő™£®10-x£©Ńĺ£¨«įÕýBĶōĶń–°Ľű≥Ķő™[7-£®10-x£©]Ńĺ£¨łýĺ›ĪŪłŮňýłÝ‘ň∑—£¨«ů≥Ųy”ŽxĶńļĮ żĻōŌĶ Ĺ£Ľ
£®3£©ĹŠļŌ“—÷™ŐűľĢ£¨«ůxĶń»°÷Ķ∑∂őߣ¨”…£®2£©ĶńļĮ żĻōŌĶ ĹĹŠļŌ“ĽīőļĮ żĶń–‘÷ «ů Ļ◊‹‘ň∑—◊Ó…ŔĶńĽű≥ĶĶųŇš∑Ĺįł£ģ
£®1£©…ŤīůĽű≥ĶxŃĺ£¨–°Ľű≥ĶyŃĺ
“ņŐ‚“‚£¨Ķ√![]() £¨Ĺ‚Ķ√
£¨Ĺ‚Ķ√![]() £¨
£¨
°ŗīůĽű≥Ķ8Ńĺ£¨–°Ľű≥Ķ7Ńĺ£Ľ
£®2£©°Ŗ«įÕýAĶōĶńīůĽű≥Ķő™xŃĺ£¨Ļ≤”–10ŃĺĽű≥Ķ«įÕýAĶō£ģ
°ŗ«įÕýAĶōĶń–°Ľű≥Ķő™£®10©Āx£©£¨«įÕýBĶōĶńīůĽű≥Ķő™£®8©Āx£©Ńĺ£¨
–°Ľű≥Ķő™[7©Ā£®10©Āx£©£Ĺx©Ā3]Ńĺ
y£Ĺ800x+400£®10©Āx£©+900£®8©Āx£©+600£®x©Ā3£©
£Ĺ800x+4000©Ā400x+7200©Ā900x©Ā1800+600x
£Ĺ100x+9400£ģ£®3°‹x°‹8£©£Ľ
£®3£©“ņŐ‚“‚£¨Ķ√900£®8©Āx£©+600£®x©Ā3£©°‹![]() [800x+400£®10©Āx£©]
[800x+400£®10©Āx£©]
’ŻņŪĶ√500x°›3400
°ŗx°›![]()
°Ŗ0°‹x°‹8£¨«“x «’Ż ż
°ŗx£Ĺ7ĽÚ8£¨
°Ŗ100£ĺ0£¨
°ŗy£Ĺ100x+9400 «‘ŲļĮ ż£ģ
°ŗĶĪx£Ĺ7 Ī£¨y◊Ó–°£Ĺ100°Ń7+9400£Ĺ10100
°ŗīň ĪĶń◊ÓĶÕ◊‹‘ň∑— «10100‘™£ģ

 ļŤÕľÕľ ťļģľŔ◊ų“ĶľŔ∆ŕ◊ų“Ķľ™Ń÷īů—ß≥Ųįś…ÁŌĶŃ–īūįł
ļŤÕľÕľ ťļģľŔ◊ų“ĶľŔ∆ŕ◊ų“Ķľ™Ń÷īů—ß≥Ųįś…ÁŌĶŃ–īūįł°ĺŐ‚ńŅ°Ņ‘ŕ°įīī»ęĻķőń√ų≥« –°ĪĽÓ∂Į÷–£¨ń≥…Á«Ýő™ŃňŃňĹ‚ĺ”√Ů’∆ő’ņ¨ĽÝ∑÷ņŗ÷™ ∂Ķń«ťŅŲĹÝ––Ķų≤ť£ģ∆š÷–A°ĘBŃĹ–°«Ý∑÷Īū”–500√Żĺ”√Ů£¨…Á«Ýī”÷–łųňśĽķ≥ť»°50√Żĺ”√ŮĹÝ––ŌŗĻō÷™ ∂≤‚ ‘£¨≤ĘĹę≥…ľ®ĹÝ––’ŻņŪĶ√ĶĹ≤Ņ∑÷–ŇŌĘ£ļ
£®–ŇŌĘ“Ľ£©A–°«Ý50√Żĺ”√Ů≥…ľ®Ķń∆Ķ ż÷Ī∑ĹÕľ»ÁÕľ£®√Ņ“Ľ◊ťļ¨«į“ĽłŲĪŖĹÁ÷Ķ£¨≤Ľļ¨ļů“ĽłŲĪŖĹÁ÷Ķ£©£Ľ
£®–ŇŌĘ∂Ģ£©Õľ÷–£¨ī”◊ůÕý”“Ķŕňń◊ťĶń≥…ľ®»ÁŌ¬
75 | 75 | 79 | 79 | 79 | 79 | 80 | 80 |
81 | 82 | 82 | 83 | 83 | 84 | 84 | 84 |
£®–ŇŌĘ»ż£©A°ĘBŃĹ–°«Ýłų50√Żĺ”√Ů≥…ľ®Ķń∆Ĺĺý ż°Ę÷–őĽ ż°Ę÷ŕ ż°Ę”Ň–„¬ £®80∑÷ľį“‘…Ōő™”Ň–„£©°Ę∑Ĺ≤ÓĶ» żĺ›»ÁŌ¬£®≤Ņ∑÷Ņ’»Ī£©£ļ
–°«Ý | ∆Ĺĺý ż | ÷–őĽ ż | ÷ŕ ż | ”Ň–„¬ | ∑Ĺ≤Ó |
A | 75.1 | 79 | 40% | 277 | |
B | 75.1 | 77 | 76 | 45% | 211 |
łý囓‘…Ō–ŇŌĘ£¨ĽōīūŌ¬Ń–ő Ő‚£ļ
£®1£©«ůA–°«Ý50√Żĺ”√Ů≥…ľ®Ķń÷–őĽ ż£ģ
£®2£©«ŽĻņľ∆A–°«Ý500√Żĺ”√Ů÷–ń‹≥¨Ļż∆Ĺĺý żĶń”–∂ŗ…Ŕ»ň£Ņ
£®3£©«Žĺ°ŃŅī”∂ŗłŲĹ«∂»Ī»ĹŌ°Ę∑÷őŲA£¨BŃĹ–°«Ýĺ”√Ů’∆ő’ņ¨ĽÝ∑÷ņŗ÷™ ∂Ķń«ťŅŲ£ģ