Question

【题目】如图，在平面直角坐标系中，，点为轴正半轴上一动点，连接，将沿翻折得，点分别为的中点，连接并延长交所在直线于点，连接．当为直角三角形时，点坐标为_______．

Answer 1

【答案】或

【解析】

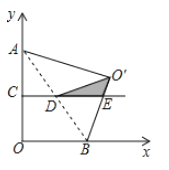
证出CD是△AOB的中位线，得出CE∥OB，由折叠的性质得出∠AO′B=∠AOB=90°，分两种情况：①当∠O′ED=90°时，则O′B⊥OB，四边形AOBO′是正方形，得出OC=CD=1，得出点D坐标为：（1，1）；
②当∠O′DE=90°时，过点D作DN⊥OB于N，证明Rt△O'DE∽Rt△BO′A，得出∠O′ED=∠BAO′，由平行线的性质得出∠O′ED=∠O′BO=2∠O′BA=2∠ABO，由得出的性质得出△ABO≌△ABO′，得出∠OAB=∠O′AB=2∠ABO，则∠ABO=30°，由直角三角形的性质得出BD=2，由勾股定理得出OB==2，得出DN=BD=1，BN==，求出ON=OB-BN=2-=，得出点D坐标为：（，1）即可．

∵点C，D分别为AO，AB的中点，
∴CD是△AOB的中位线，
∴CE∥OB，
∵△ABO沿AB翻折得到△ABO'，
∴∠AO′B=∠AOB=90°，
∴当△O'DE为直角三角形时，∠O′ED=90°或∠O′DE=90°，
①当∠O′ED=90°时，如图1所示：
则O′B⊥OB，四边形AOBO′是正方形，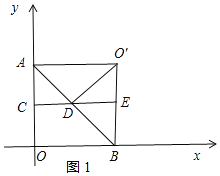

∵A（0，2），
∴OC=CD=1，
∴点D坐标为：（1，1）；
②当∠O′DE=90°时，过点D作DN⊥OB于N，如图2所示：

∵点D是AB的中点，
∴O′D=BD，
∴∠DO′E=∠DBO′，
∵∠O′DE=∠AO′B=90°，
∴Rt△O'DE∽Rt△BO′A，
∴∠O′ED=∠BAO′，
∵CE∥OB，
∴∠O′ED=∠O′BO=2∠O′BA=2∠ABO，
∵△ABO与△ABO′关于直线AB对称，
∴△ABO≌△ABO′，
∴∠OAB=∠O′AB=2∠ABO，
∴∠ABO=30°，
∵A（0，2），
∴OA=2，
∴AB=4，
∴BD=2，OB=，
∴DN=BD=1，BN=，
∴ON=OB-BN=2-=，
∴点D坐标为：（，1）；
综上所述，点D坐标为：（1，1）或（，1）；
故答案为：（1，1）或（，1）．