题目内容
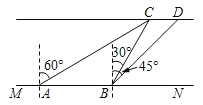
【题目】小明想要测量水面人工岛上两棵小树CD的距离,如图,已知河岸MN∥CD,小明在河岸MN上点A处测量小树C位于北偏东60°方向,然后沿河岸走了20米,到达点B处,此时测得河对岸小树C位于北偏东30°方向,小树D位于东北方向,则两棵树CD的距离为_____米.(结果保留根号)
【答案】(10![]() ﹣10)
﹣10)
【解析】
作CE⊥MN于点E、DF⊥MN于点F,设BE=a,利用三角函数求得![]() ,再由tan∠CAE=
,再由tan∠CAE=![]() 列方程求得a=10,据此知BE=10,DF=CE=10
列方程求得a=10,据此知BE=10,DF=CE=10![]() ,继而由∠DBF=45°知BF=DF=10
,继而由∠DBF=45°知BF=DF=10![]() ,从而得出答案.
,从而得出答案.
如图所示,过点C作CE⊥MN于点E,过点D作DF⊥MN于点F,
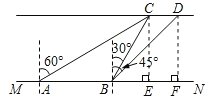
设BE=a,
在Rt△BCE中,∵∠BCE=30°,
∴CE=![]() =
=![]() =
=![]() a,
a,
在Rt△ACE中,∵∠CAE=30°,AB=20,
∴由tan∠CAE=![]() 可得
可得![]() =
=![]() ,
,
解得a=10,
∴BE=10,DF=CE=10![]() ,
,
在Rt△BDF中,∵∠DBF=45°,
∴BF=DF=10![]() ,
,
∴CD=EF=BF﹣BE=10![]() ﹣10(米),
﹣10(米),
故答案为:(10![]() ﹣10).
﹣10).

练习册系列答案
相关题目