题目内容
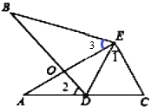
【题目】如图,![]() ,
,![]() ,点
,点![]() 在
在![]() 边上,
边上,![]() .
.
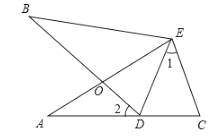
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的度数;
的度数;
(3)若![]() ,当
,当![]() 的外心在直线
的外心在直线![]() 上时,
上时,![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)结合已知,要证明![]() 还少一个条件,可以在
还少一个条件,可以在![]() 和
和![]() 中结合对顶角和三角形内角和得到
中结合对顶角和三角形内角和得到![]() ,进一步得到
,进一步得到![]() ,即可证明.
,即可证明.
(2)第(1)题已经证明![]() ,再根据
,再根据![]() ,得到
,得到![]() ,所以在等腰
,所以在等腰![]() 求
求![]() 即可.
即可.
(3)根据“直角圆周角所对的弦为直径” 且![]() 的外心在直线
的外心在直线![]() 上,则
上,则![]() 与
与![]() 的交点
的交点![]() 即为
即为![]() 的外心,再根据“直角三角形斜边上的中线等于斜边的一半”得到
的外心,再根据“直角三角形斜边上的中线等于斜边的一半”得到![]() ,故
,故![]() 是等边三角形,再用特殊角的三角函数求
是等边三角形,再用特殊角的三角函数求![]() 即可.
即可.
解:(1)∵![]() 和
和![]() 相交于点
相交于点![]() ,
,
∴![]() .
.
又∵在![]() 和
和![]() 中,
中,![]() ,
,
∴![]() .
.
又∵![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
在![]() 和
和![]() 中,
中,
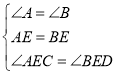 ,
,
∴![]() .
.
(2)∵![]()
∴![]()
又∵![]()
∴![]()
∴![]()
∴![]()
(3)∵![]() ,且
,且![]() 的外心在直线
的外心在直线![]() 上
上
∴点![]() 是
是![]() 的外心(或
的外心(或![]() 是
是![]() 中点)
中点)
∴![]()
又∵![]()
∴![]() 是等边三角形
是等边三角形
∴![]()
在![]() 中,
中,![]()
∴![]()

练习册系列答案
相关题目