题目内容
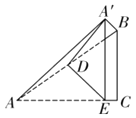
【题目】点A是函数y=![]() (x>0)上一动点,连接OA,线段OB与OA关于y轴对称,将线段OA绕点O逆时针旋转90°得线段OC,将线段OA绕点A逆时针旋转90°得线段DA.
(x>0)上一动点,连接OA,线段OB与OA关于y轴对称,将线段OA绕点O逆时针旋转90°得线段OC,将线段OA绕点A逆时针旋转90°得线段DA.

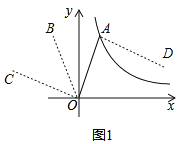
(1)在图1中画出线段OB、OC,保留作图痕迹;
(2)连接AB、BC、AC,当△AOB的面积等于△BOC的面积时,求△ABC的面积;
(3)如图3,若点D的坐标为(m,n),直接写出m与n的等量关系式.
【答案】(1)详见解析;(2)2![]() 或2
或2![]() +4;(3)m2﹣n2=8+8
+4;(3)m2﹣n2=8+8![]() .
.
【解析】
(1)由旋转的性质和轴对称的性质可得;
(2)分OB在∠AOC内部和外部两种情况讨论,先求出OA2=OB2=OC2=4![]() +8,再利用面积和差关系可求解;
+8,再利用面积和差关系可求解;
(3)过点A作AE⊥x轴于点E,过点D作DF⊥AE于F,由AAS可证△AOE≌△DAF,可得AE=DF,OE=AF,即可求OE=![]() ,AE=
,AE=![]() ,由反比例函数的性质可求解.
,由反比例函数的性质可求解.
解:(1)如图所示:
(2)∵线段OB与OA关于y轴对称,将线段OA绕点O逆时针旋转90°得线段OC,
∴OA=OB=OC,∠AOC=90°,
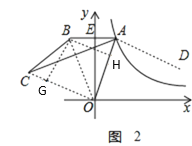
①当OB在∠AOC内部时,如图2,作BH⊥OA于H,BG⊥OC于G,设AB交y轴于点E,
∵点A是函数y=![]() (x>0)上一动点,
(x>0)上一动点,
∴S△AOE=![]() (2+2
(2+2![]() ),
),
∴S△AOB=2+2![]() ,
,
∵△AOB的面积等于△BOC的面积,
∴![]() OA×BH=
OA×BH=![]() OC×BG,且OC=OA,
OC×BG,且OC=OA,
∴BH=BG,且BH⊥OA,BG⊥OC,
∴OB平分∠AOC,
∴∠AOB=45°,且BH⊥AO,
∴∠HOB=∠HBO,
∴BH=OH
∴BH=OH=![]() OB=
OB=![]() OA,
OA,
∵S△AOB=![]() AO×BH,
AO×BH,
∴2+2![]() =
=![]() ×OA×
×OA×![]() OA,
OA,
∴OA2=4![]() +8,
+8,
∵S△ABC=S△ABO+S△BOC﹣S△ACO,
∴S△ABC=2×(2+2![]() )﹣
)﹣![]() ×AO2=2
×AO2=2![]()
②当OB在∠AOC外部时,如图2﹣1,过点C作CH⊥BO于H,作AG⊥BO于G,
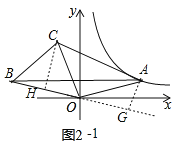
∵△AOB的面积等于△BOC的面积,
∴![]() OB×CH=
OB×CH=![]() OB×AG,
OB×AG,
∴CH=AG,且CH∥AG,
∴四边形ACHG是平行四边形,
∴AC∥HG,
∴∠ACO=∠COB=45°,
∴∠HCO=∠HOC=45°,
∴CH=OH,
∴CH=![]() OC=
OC=![]() OB,
OB,
∵S△BOC=![]() BO×CH=2+2
BO×CH=2+2![]() ,
,
∴BO2=4![]() +8=OC2,
+8=OC2,
∵S△ABC=S△BOC+S△AOC﹣S△AOB=S△AOC,
∴S△ABC=![]() OC2=2
OC2=2![]() +4,
+4,
(3)如图3,过点A作AE⊥x轴于点E,过点D作DF⊥AE于F,

∵将线段OA绕点A逆时针旋转90°得线段DA,
∴DA=OA,∠OAD=90°,
∴∠OAE+∠DAF=90°,且∠DAF+∠ADF=90°,
∴∠OAE=∠ADF,且∠AEO=∠AFD=90°,AO=AD,
∴△AOE≌△DAF(AAS)
∴AE=DF,OE=AF,
∵点D的坐标为(m,n),
∴OE+DF=m,AF﹣AE=﹣n,
∴OE=![]() ,AE=
,AE=![]() ,
,
∵OEAE=2+2![]() ,
,
∴m2﹣n2=8+8![]() .
.

 阅读快车系列答案
阅读快车系列答案