题目内容
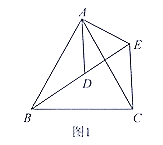
【题目】如图，在四边形ABCD中，已知AB＝AD＝2，BC＝3，CD＝1，∠A＝90°．
（1）求BD的长；
（2）求∠ADC的度数．
【答案】（1）2
；（2）135°．
【解析】
（1）首先在Rt△BAD中，利用勾股定理求出BD的长；
（2）根据等腰直角三角形的性质求出∠ADB＝45°，再根据勾股定理逆定理在△BCD中，证明△BCD是直角三角形，即可求出答案．
解：（1）在Rt△BAD中，
∵AB＝AD＝2，
∴BD＝
＝
＝2；
（2）在Rt△BAD中，
∵AB＝AD＝2，
∴∠ADB＝45°，
在△BCD中，
DB2+CD2＝8+12＝9＝CB2，
∴△BCD是直角三角形，
∴∠BDC＝90°，
∴∠ADC＝∠ADB+∠BDC＝45°+90°＝135°．
练习册系列答案
同步轻松练习系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
【题目】某直销公司现有
名推销员，
月份每个人完成销售额（单位：万元），数据如下：
整理上面的数据得到如下统计表：
销售额 |
|
|
|
|
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
|
|
|
|
（1）统计表中的
；
；
（2）销售额的平均数是 ；众数是 ；中位数是 .
（3）
月起，公司为了提高推销员的积极性，将采取绩效工资制度：规定一个基本销售额，在基本销售额内，按
抽成；从公司低成本与员工愿意接受两个层面考虑，你认为基本销售额定位多少万元？请说明理由.
