题目内容
【题目】在△ABC中,∠A=50°,点D,E分别是边AC,AB上的点(不与A,B,C重合),点P是平面内一动点(P与D,E不在同一直线上),设∠PDC=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在边BC上运动(不与点B和点C重合),如图(1)所示,则∠1+∠2=________
(用α的代数式表示).
(2)若点P在ABC的外部,如图(2)所示,则∠α,∠1,∠2之间有何关系?写出你的结论,并说明理由.
(3)当点P在边CB的延长线上运动时,试画出相应图形,标注有关字母与数字,并写出对应的∠α,∠1,∠2之间的关系式.(不需要证明)

【答案】(1)∠1+∠2=50°+∠α;
(2)∠2﹣∠1=∠α﹣50°;
(3) ①∠2﹣∠1=∠α﹣50°;②∠1﹣∠2=50°+∠α.
【解析】(1)∵∠AEP=180°﹣∠2,∠ADP=180°﹣∠1,
∴180°﹣∠2+180°﹣∠1+∠α+50°=360°,
即∠1+∠2=50°+∠α;
(2)根据三角形外角的性质可知,
∠2﹣∠α=∠1﹣50°,
则∠2﹣∠1=∠α﹣50°;
(3)如图, ①∠2﹣∠α=∠1﹣50°,则∠2﹣∠1=∠α﹣50°;
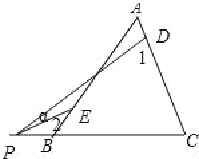
如图,②∠1=50°+∠α+∠2,∠1﹣∠2=50°+∠α.


练习册系列答案
相关题目