题目内容
【题目】如图，AD是△ABC的中线，E，F分别是AD和AD延长线上的点，且DE=DF，连结BF，CE.下列说法：①△ABD和△ACD面积相等；②∠BAD=∠CAD；③△BDF≌△CDE；④BF∥CE；其中正确的有（ ）
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
根据三角形中线的定义可得BD=CD，根据等底等高的三角形的面积相等判断出①正确，然后利用“边角边”证明△BDF和△CDE全等，可判断出③正确；根据全等三角形对应角相等可得∠F=∠CED，再根据内错角相等，两直线平行可得BF∥CE，可判断出④正确．
∵BD=CD，点A到BD、CD的距离相等，
∴△ABD和△ACD面积相等，故①正确；
∵AD为△ABC的中线，
∴BD=CD，∠BAD和∠CAD不一定相等，故②错误；
在△BDF和△CDE中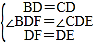
，
∴△BDF≌△CDE，故③正确；
∴∠F=∠DEC，
∴BF∥CE，故④正确；
故选：C．
练习册系列答案
导学教程高中新课标系列答案
小学课时特训系列答案
相关题目
