题目内容
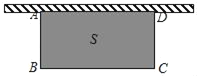
【题目】如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.

(1)求证:△ABM ∽△EMA;
(2)若AB=2,BM=1,求DE的长.
【答案】(1)详见解析;(2)3
【解析】
(1)利用三角形两组对应角相等,可证三角形相似;
(2)先用勾股定理求出AM,在根据三角形相似的性质求出AE,最后DE=AE-AD即可求解.
解:(1)∵四边形ABCD是正方形,
∴∠ABC=90°
∵ME⊥AM,
∴∠AME=90°,
∴∠AMB+∠BAM=90°,∠BAM+∠EAM=90°,
∴∠AMB =∠EAM,∠ABC=∠AME =90°
.∴△ABM ∽△EMA,
(2)∵AB=2,BM=1
∴AM=![]()
∵△ABM ∽△EMA
∴![]() 即:
即:![]() ,解得AE=5;
,解得AE=5;
又∵四边形ABCD是正方形,
∴AD=AB=2
∴DE=AE-AD=5-2=3

练习册系列答案
相关题目
【题目】已知二次函数y=x2+2x﹣3.
(1)把函数配成y=a(x﹣h)2+k的形式;
(2)求函数与x轴交点坐标;
(3)用五点法画函数图象
x | … | … | |||||
y | … | … |
(4)当y>0时,则x的取值范围为_____.
(5)当﹣3<x<0时,则y的取值范围为_____.