题目内容
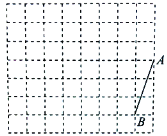
【题目】如图,方格纸中每个小正方形的边长均为1,线段AB的端点均在小正方形的顶点上.
(1)在图中画出以线段AB为一边的矩形ABCD(不是正方形),且点C和点D均在小正方形的顶点上;
(2)在图中画出以线段AB为一腰,底边长为![]() 的等腰三角形ABE,点E在小正方形的顶点,则CE= ;
的等腰三角形ABE,点E在小正方形的顶点,则CE= ;
(3)F是边AD上一动点,则CF+EF的最小值是 .
【答案】(1)作图见解析;(2)4;(3)2![]() .
.
【解析】
(1)根据矩形的性质结合网格特点作图即可;
(2)首先作图符合题意的△ABE,根据图形易得CE;
(3)作C点关于AD对称的点C’,连接EC’交AD于点F,则EC’的长即为CF+EF的最小值,用勾股定理求出EC’即可.
解:(1)如图所示:矩形ABCD即为所求;
(2)如图所示:等腰三角形ABE即为所求,易得CE=4;
(3)作C点关于AD对称的点C’,连接EC’交AD于点F,则EC’的长即为CF+EF的最小值,EC’=![]() ,则CF+EF的最小值是
,则CF+EF的最小值是![]() .
.


练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目