��Ŀ����
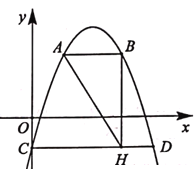
����Ŀ���ȱߡ�ABC��������DEFG��ͼ1���ã�����D��E����ֱ���AB��BC�ϣ���BD��BE��
��1�����DEB�Ķ�����
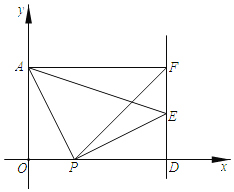
��2����������DEFG��������BC������ÿ��1����λ���ȵ��ٶ�ƽ��ʱ��CF�ij���y�����˶�ʱ��仯�ĺ���ͼ����ͼ2��ʾ���ҵ�t=![]() ʱ��y����Сֵ1��
ʱ��y����Сֵ1��
����ȱߡ�ABC�ı߳���
������CD����ƽ�ƵĹ����У���CEF���CDEͬʱΪ����������ʱt��ֵ��
����ƽ���˶���ʼ����GFǡ����AC����ʱ����ֱ��д����CEF���ԲԲ�ĵ��˶�·���ij��ȣ�
���𰸡���1����BED��60�㣻��2����2+2![]() ����t��2
����t��2![]() ��2��2+2
��2��2+2![]() ����
����![]() ��
��
��������
��1��֤����BDE�ǵȱ������μ��ɽ�����⣮
��2������ͼ2�У�������DEFGƽ�ƹ����У�FF���BC����֤�ı���EFF��E����ƽ���ı��Σ������⣬��CF���BCʱ��CF���ֵ��С����ʱCF�䣽1����ֱ�����������E��F�䣬CE�伴�ɣ�
�����������ηֱ�ͼ����⼴�ɣ�
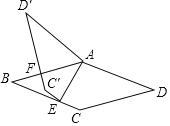
����ͼ5�У����CE��F������Բ��Բ��ΪI������IE�䣬CI��IF�䣬��ֱ��FF�佻AC��H����CB��ȡһ��J��ʹ��CH��CJ������JH��IJ��֤����HCF��ա�JCI��SAS�����Ƴ�JI��HF�䣬���ɽ�����⣮
�⣺��1����ͼ1�У�

�ߡ�ABC�ǵȱ������Σ�
���B��60�㣬
��BD��BE��
���BDE�ǵȱ������Σ�
���BED��60�㣮
��2������ͼ2�У�

��ͼ������DEFGƽ�ƹ����У�FF���BC����֤�ı���EFF��E����ƽ���ı��Σ�
�����⣬��CF���BCʱ��CF���ֵ��С����ʱCF�䣽1��
��Rt��CE��F���У��ߡ�E��CF�䣽90�㣬��F��E��C��30�㣬CF�䣽1��
��EF��E��F�䣽2��CE�䣽![]() ��
��
��t��EE�䣽![]() ��
��
��EE�䣽CE�䣽![]() ��
��
��BE��DE��EF��2��
��BC��BE+EE��+CE�䣽2+2![]() ��
��
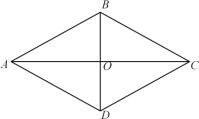
����ͼ3�У���E��D�䣽E��F�䣽CE�䣽2ʱ����CEF���CDEͬʱΪ���������Σ���ʱt��EE�䣽BC��BE��CE�䣽2+2![]() ��4��2
��4��2![]() ��2��
��2��

��ͼ4�У���E��C��E��D�䣽E��F�䣽2ʱ����CEF���CDEͬʱΪ���������Σ���ʱt��EE�䣽BC+CE�䩁BE��BC��2+2![]() ��
��

����������t��2![]() ��2��2+2
��2��2+2![]() ʱ����CEF���CDEͬʱΪ���������Σ�
ʱ����CEF���CDEͬʱΪ���������Σ�
����ͼ5�У����CE��F������Բ��Բ��ΪI������IE�䣬CI��IF�䣬��ֱ��FF�佻AC��H����CB��ȡһ��J��ʹ��CH��CJ������JH��IJ��

��IE�䣽IF�䣽IC��
���F��E��C��![]() ��F��IC��
��F��IC��
�ߡ�F��E��C��30�㣬
���CJF�䣽60�㣬
���CIF���ǵȱ������Σ�
��CH��CJ����HCJ��60�㣬
���HCJ�ǵȱ������Σ�
��CH��CJ��CF�䣽CI����HCJ����F��CI��60�㣬
���HCF�䣽��JCI��
���HCF��ա�JCI��SAS����
��F��H��IJ����CHF�䣽��CJI��120�㣬
���I���˶��켣���߶Σ���JI��HF�䣬
������֪FH��![]() ��
��
���CEF���ԲԲ�ĵ��˶�·���ij���Ϊ![]() ��
��