Question

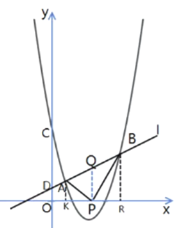
【题目】如图，在平面直角坐标系中，抛物线与直线交于A（1,1），B两点，与轴交于点C，直线与轴交于点D．

（1）求抛物线的对称轴和点C的坐标；

（2）若在轴上有且只有一点P，使∠APB=90°，求的值；

（3）设直线与抛物线的对称轴的交点为F，G是抛物线上位于对称轴右侧的一点，若，且△BCG与△BCD的面积相等，求点G的坐标.

Answer 1

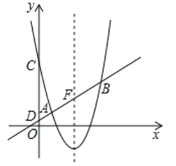
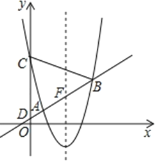
【答案】（1）对称轴是x=2.5 ， C的坐标为（0,5）；（2）k=；（3）点G的坐标为（3，-1）或（）

【解析】

（1）根据对称轴公式即可求出对称轴，根据常数项可得C点坐标；

（2）过点A作AK⊥x轴于点K，过B作BR⊥x轴于点R，设B（p，q），通过△AKP∽△PRB得到q=，然后根据q=p-5p+5可解得p1=2（舍去），p2=4，然后用待定系数法可求出k的值；

（3）过点A作AM⊥对称轴于点M，过点B作BN⊥对称轴于点N，构造相似三角形求出B的坐标，从而得到直线AB与直线BD的解析式，求出点D坐标，设点D关于点C的对称点为D′，则 D′（0，），所以点G在过点D或D′，平行线于BC的直线上，然后联立一次函数与抛物线的解析式即可求出符合题意的点G坐标

解：（1）对称轴是x=2.5

C的坐标为（0,5）

（2）∵在x轴上有且仅有一点P，使∠APB=90，

∴以AB为直径的圆与x轴相切，取AB中点Q，作QP⊥x轴，垂足为P，

过点A作AK⊥x轴于点K，过B作BR⊥x轴于点R，构造“三垂直模型”

设B（p，q），则Q（，），

P（，0），K（1，0），R（p，0），

△AKP∽△PRB，AK∶RP=KP∶BR，

∴ 1∶（p-）=(-1)∶q，

化简，得：q=，

∴2= p-5p+5，

解得：p1=2，p2=4；

当p=2时，q=＜1，k＜0，与题中条件k＞0矛盾，

∴B（4，），代入直线l解析式：/p>

4k+m=；

又直线l过A（1，1），

∴k+m=1，

联立方程组，解得：k=;

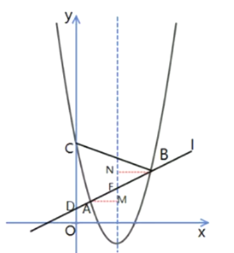
（3）过点A作AM⊥对称轴于点M，过点B作BN⊥对称轴于点N，

∵AF：FB=3:4，∴AM∶BN=3∶4，

∵AM=-1=，

∴BN=2，即点B的横坐标为2+=；

B的纵坐标为：（）-5×+5=，

∴B（，）；

将A、B坐标代入l解析式：

k+m=1；

+m=，

解得：k=，m=，

∴D（0，）；

∴直线BC解析式为：+5；

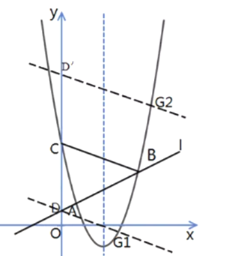
设点D关于点C的对称点为D′，则 D′（0，）,

∵△BCD和△BCG有公共边BC，

∴点G在过点D或D′，平行线于BC的直线上,

分别作DG1∥BC，D′G2∥BC，G1、G2在抛物线上

DG 1解析式：y=+，与y= x-5x+5联立，

解得：x1=，x2=3，

∵G在对称轴右侧，

∴x=3，y=-1，

∴G1（3，-1）；

D′G2解析式：y=+，与y= x-5x+5联立，

解得：x1=，x2=（舍去），

∴x=，y=，

∴G2（，）,

综上所述，点G的坐标为：（3，-1）；或（，）,