题目内容
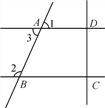
【题目】已知点O为直线AB上的一点,∠EOF为直角,OC平分∠BOE.
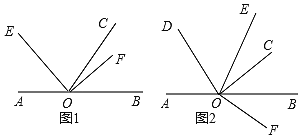
(1)如图1,若∠AOE=45°,写出∠COF等于多少度;
(2)如图1,若∠AOE=![]() 求∠COF的度效(用含
求∠COF的度效(用含![]() 的代数式表示);
的代数式表示);
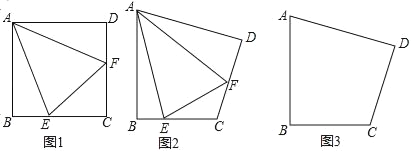
(3)如图2,若∠AOE=![]() OD平分∠AOC,且∠AOD-∠BOF=45°,求
OD平分∠AOC,且∠AOD-∠BOF=45°,求![]() 的值。
的值。
【答案】(1)22.5° (2)![]() n° (3) 120
n° (3) 120
【解析】
(1)由∠AOE=45°,可以求得∠BOE=135°,再由OC平分∠BOE,可求得∠COE=67.5°,∠EOF为直角,所以可得∠COF=∠EOF-∠EOC=22.5°;
(2)由(1)的方法即可得到∠COF=![]() n°;
n°;
(3)先设∠BOF为x°,再根据角的关系得出方程,解答后求出n的值即可.
解:(1)∵∠AOE=45°,
∴∠BOE=135°,
∵OC平分∠BOE,
∴∠COE=67.5°,
∵∠EOF为直角,
∴∠COF=∠EOF-∠EOC=22.5°,
(2))∵∠AOE=n°,
∴∠BOE=180°-n°,
∵OC平分∠BOE,
∴∠COE=![]() (180°-n°),
(180°-n°),
∵∠EOF为直角,
∴∠COF=∠EOF-∠EOC=90°-![]() (180°-n°)=
(180°-n°)=![]() n°,
n°,
(3)设∠BOF为x°,∠AOD为(x+45)°,∠EOB为(90-x)°,OC平分∠BOE,
则可得:∠AOD+∠DOC+∠EOB=∠AOB+∠EOC.
x+45+x+45+90-x=180+![]() (90-x),
(90-x),
解得:x=30,
所以可得:∠EOB=(90-x)°=60°,
∠AOE=180°-∠EOB=180°-60°=120°,
故n的值是120.

练习册系列答案
相关题目