题目内容
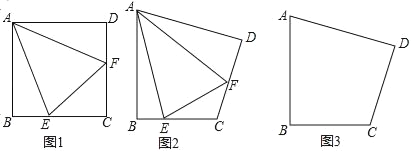
【题目】已知在四边形ABCD中,点E、F分别是BC、CD边上的一点.
(1)如图1:当四边形ABCD是正方形时,且∠EAF=45°,则EF、BE、DF满足的数量关系是 ,请说明理由;
(2)如图2:当AB=AD,∠B=∠D=90°,∠EAF是∠BAD的一半,问:(1)中的数量关系是否还存在? (填是或否)
(3)在(2)的条件下,将点E平移到BC的延长线上,请在图3中补全图形,并写出EF、BE、DF的关系.
【答案】(1)EF=BE+DF,理由详见解析;(2)是;(3)图详见解析,EF=BE﹣DF.
【解析】
(1)先判断出△ABM≌△ADF,进而得出AM=AF,∠BAM=∠DAF,然后由∠EAF=45°,证得∠EAM=∠EAF,继而证得△EAM≌△EAF,继而证得结论;
(2)首先延长CB到P使BP=DF,证得△ABP≌△ADF(SAS),再证得△APE≌△AFE(SAS),继而证得结论;
(3)首先在BC上截取BP=DF,证得△ABP≌△ADF(SAS),再证得△APE≌△AFE(SAS),即可得EF=BE﹣BP=BE﹣DF.
解:(1)EF=BE+DF,
理由:如图1,延长CB至M,使BM=DF,
∵四边形ABCD是正方形,
∴AB=AD,∠ABM=∠D=90°,
在△ABM和△ADF中,
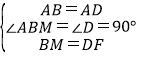 ,
,
∴△ABM≌△ADF(SAS),
∴AM=AF,∠BAM=∠DAF,
∵四边形ABCD是正方形,∠EAF=45°,
∴∠DAF+∠BAE=45°,
∴∠EAM=∠BAM+∠BAE=45°,
∴∠EAM=∠EAF,
在△EAM和△EAF中,
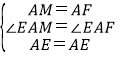 ,
,
∴△EAM≌△EAF(SAS),
∴EF=EM=BM+BE=BE+DF;
故答案为:EF=BE+DF;
(2)是存在,
理由如下:延长CB到P使BP=DF,
∵∠ABC=∠D=90°,
∴∠ABP=90°,
∴∠ABP=∠D,
在△ABP和△ADF中,
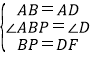 ,
,
∴△ABP≌△ADF(SAS),
∴AP=AF,∠BAP=∠DAF,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠BAE+∠DAF=∠EAF,
∴∠BAP+∠FAD=∠EAF,
即:∠EAP=∠EAF,
在△APE和△AFE中,
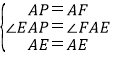 ,
,
∴△APE≌△AFE(SAS),
∴PE=FE,
∴EF=BE+DF;
故答案为:是;
(3)如图3,补全图形.
证明:在BC上截取BP=DF,
∵∠B=∠ADC=90°,
∴∠ADF=90°,
∴∠B=∠ADF,
在△ABP和△ADF中,
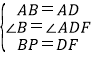 ,
,
∴△ABP≌△ADF(SAS),
∴AP=AF,∠BAP=∠DAF,
∵∠EAF=![]() ∠BAD,
∠BAD,
∴∠DAE+∠DAF=![]() ∠BAD,
∠BAD,
∴∠BAP+∠EAD=![]() ∠BAD,
∠BAD,
∴∠EAP=![]() ∠BAD=∠EAF,
∠BAD=∠EAF,
在△APE和△AFE中,
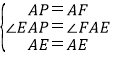 ,
,
∴△APE≌△AFE(SAS),
∴PE=FE,
∴EF=BE﹣BP=BE﹣DF.

 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案