题目内容
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB、BC于点E、F、G,连接ED、DG. 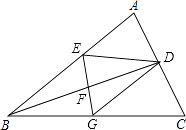
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2,求GC的长.
【答案】
(1)解:四边形EBGD是菱形.
理由:∵EG垂直平分BD,
∴EB=ED,GB=GD,
∴∠EBD=∠EDB,
∵∠EBD=∠DBC,
∴∠EDF=∠GBF,
在△EFD和△GFB中,
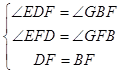 ,
,
∴△EFD≌△GFB,
∴ED=BG,
∴BE=ED=DG=GB,
∴四边形EBGD是菱形
(2)解:作DH⊥BC于H,
∵四边形EBGD为菱形ED=DG=2,
∴∠ABC=30°,∠DGH=30°,
∴DH=1,GH= ![]() ,
,
∵∠C=45°,
∴DH=CH=1,
∴CG=GH+CH=1+ ![]() .
.
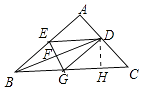
【解析】(1)结论四边形EBGD是菱形.只要证明BE=ED=DG=GB即可.(2)作DH⊥BC于H,由四边形EBGD为菱形ED=DG=2,求出GH,CH即可解决问题.
【考点精析】通过灵活运用线段垂直平分线的性质,掌握垂直于一条线段并且平分这条线段的直线是这条线段的垂直平分线;线段垂直平分线的性质定理:线段垂直平分线上的点和这条线段两个端点的距离相等即可以解答此题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目