Question

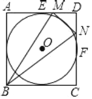
【题目】如图，⊙O内切于正方形ABCD，边AD、CD分别与⊙O切于点E、F，点M、N分别在线段DE、DF上，且MN与⊙O相切，若△MBN的面积为8，则⊙O的半径为（　　）

A.B.2C.D.2

Answer 1

【答案】B

【解析】

设⊙O与MN相切于点K，设正方形的边长为2a．因为AD、CD、MN是切线，可得AE=DE=DF=CF=a，MK=ME，NK=NF，设MK=ME=x，NK=NF=y，在Rt△DMN中，以为MN=x+y，DN=a-y，DM=a-x，看到（x+y）2=（a-y）2+（a-x）2，推出ax+ay+xy=a2，根据S△BMN=S正方形ABCD-S△ABM-S△DMN-S△BCN=8，构建方程求出a即可解决问题；

解：设⊙O与MN相切于点K，设正方形的边长为2a．

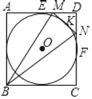
∵AD、CD、MN是切线，

∴AE＝DE＝DF＝CF＝a，MK＝ME，NK＝NF，设MK＝ME＝x，NK＝NF＝y，

在Rt△DMN中，∵MN＝x+y，DN＝a﹣y，DM＝a﹣x，

∴（x+y）2＝（a﹣y）2+（a﹣x）2，

∴ax+ay+xy＝a2，

∵S△BMN＝S正方形ABCD﹣S△ABM﹣S△DMN﹣S△BCN＝8，

∴4a2﹣×2a×（a+x）﹣（a﹣x）（a﹣y）﹣×2a×（a+y）＝8，

∴a2﹣（ax+ay+xy）＝8，

∴a2＝8，

∴a＝2，

∴AB＝2a＝4，

∴⊙O的半径为2，

故选：B．