题目内容
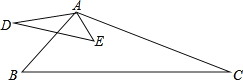
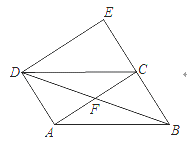
【题目】如图,ABCD中,点E在BC延长线上,EC=BC,连接DE,AC,AC⊥AD于点A、
(1)求证:四边形ACED是矩形;
(2)连接BD,交AC于点F.若AC=2AD,猜想∠E与∠BDE的数量关系,并证明你的猜想.
【答案】(1)证明见解析(2)∠E=2∠BDE
【解析】
(1)由四边形ABCD是平行四边形,EC=BC,易证得四边形ACED是平行四边形,又由AC⊥AD,即可证得四边形ACED是矩形;
(2)根据矩形的性质得∠E=∠DAC=90°,可证得DA=AF,由等腰三角形的性质可得∠ADF=45°,则∠BDE=45°,可得出∠E=2∠BDE.
(1)证明:因为ABCD是平行边形,
∴AD=BC,AD∥BC,
∵BC=CE,点E在BC的延长线上,
∴AD=EC,AD∥EC,
∴四边形ACED为平行四边形,
∵AC⊥AD,
∴平行四边形ACED为矩形
(2)∠E=2∠BDE
理由:∵平行四边形ABCD中,AC=2AF,
又∵AC=2AD,
∴AD=AF,
∴∠ADF=∠AFD,
∵AC∥ED,
∴∠BDE=∠BFC,
∵∠BFC=∠AFD,
∴∠BDE=∠ADF=45°,
∴∠E=2∠BDE

练习册系列答案
相关题目
【题目】某校为实施国家“营养早餐”工程,食堂用甲、乙两种原料配制成某种营养食品,已知这两种原料的维生素C含量及购买这两种原料的价格如表:
原科维生素C及价格 | 甲种原料 | 乙种原料 |
维生素c(单位/千克) | 600 | 400 |
原料价格(元/千克) | 9 | 5 |
现要配制这种营养食品20千克,设购买甲种原料x千克,购买这两种原料的总费用为y元.
(1)求y与x的函数关系式?
(2)若食堂要求营养食品每千克至少含有480单位的维生素C,试说明需要购买甲种原料多少千克时,总费用最少?最少费用是多少元?