ΧβΡΩΡΎ»ί
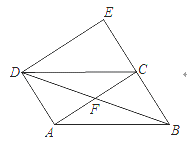
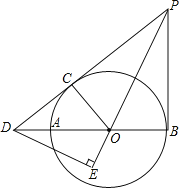
ΓΨΧβΡΩΓΩ»γΆΦΘ§±Ώ≥ΛΈΣ4ΒΡ’ΐΖΫ–ΈABCD÷–Θ§ΒψP «±ΏCD…œ“ΜΕ·ΒψΘ§Ής÷±œΏBPΘ§ΙΐAΓΔCΓΔD»ΐΒψΖ÷±πΉς÷±œΏBPΒΡ¥ΙœΏΕΈΘ§¥ΙΉψΖ÷±π «EΓΔFΓΔGΘ°
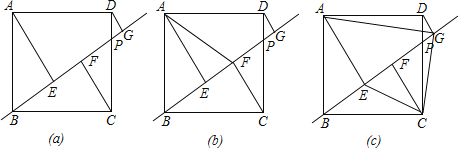
Θ®1Θ©»γΆΦΘ®aΘ©Υυ ΨΘ§Β±CPΘΫ3 ±Θ§«σœΏΕΈEGΒΡ≥ΛΘΜ
Θ®2Θ©»γΆΦΘ®bΘ©Υυ ΨΘ§Β±ΓœPBCΘΫ30Γψ ±Θ§ΥΡ±Ώ–ΈABCFΒΡΟφΜΐΘΜ
Θ®3Θ©»γΆΦΘ®cΘ©Υυ ΨΘ§ΒψP‘ΎCD…œ‘ΥΕ·ΒΡΙΐ≥Χ÷–Θ§ΥΡ±Ώ–ΈAECGΒΡΟφΜΐS «Ζώ¥φ‘ΎΉν¥σ÷ΒΘΩ»γΙϊ¥φ‘ΎΘ§«κ«σ≥ωΓœPBCΈΣΕύ…ΌΕ» ±Θ§S”–Ήν¥σ÷ΒΘ§Ήν¥σ÷Β «Εύ…ΌΘΩ»γΙϊ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©![]() ΘΜΘ®2Θ©6+2
ΘΜΘ®2Θ©6+2![]() ΘΜΘ®3Θ©Β±ΓœPBCΈΣ22.5Γψ ±Θ§S”–Ήν¥σ÷ΒΘ§Ήν¥σ÷Β «4+4
ΘΜΘ®3Θ©Β±ΓœPBCΈΣ22.5Γψ ±Θ§S”–Ήν¥σ÷ΒΘ§Ήν¥σ÷Β «4+4![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©―”≥ΛAEΫΜBC”ΎΒψQΘ§ΙΐΒψDΉςDRΓΆAEΘ§”…Χβ“βΩ…÷ΛΥΡ±Ώ–ΈDREG «ΨΊ–ΈΘ§Φ¥DRΘΫEGΘ§”…Ι¥Ι…Ε®άμΩ…«σBPΘΫ5Θ§”…Β»Ϋ«ΒΡ”ύΫ«œύΒ»Ω…ΒΟΓœADRΘΫΓœPBQΘ§Ω…÷ΛΓςADRΓΉΓςPBCΘ§Ω…ΒΟ![]() ,Ω…«σ≥ωDRΘΫ
,Ω…«σ≥ωDRΘΫ![]() Θ§Φ¥EGΘΫ
Θ§Φ¥EGΘΫ![]() ΘΜΘ®2Θ©ΙΐΒψFΉςFMΓΆAB”ΎΒψMΘ§ΉςFNΓΆBC”ΎΒψNΘ§”…Χβ“βΩ…÷ΛΥΡ±Ώ–ΈBNFM «ΨΊ–ΈΘ§Ω…ΒΟFMΘΫBNΘ§”…÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ Ω…«σCFΘΫ2Θ§NCΘΫ1Θ§FNΘΫ
ΘΜΘ®2Θ©ΙΐΒψFΉςFMΓΆAB”ΎΒψMΘ§ΉςFNΓΆBC”ΎΒψNΘ§”…Χβ“βΩ…÷ΛΥΡ±Ώ–ΈBNFM «ΨΊ–ΈΘ§Ω…ΒΟFMΘΫBNΘ§”…÷±Ϋ«»ΐΫ«–ΈΒΡ–‘÷ Ω…«σCFΘΫ2Θ§NCΘΫ1Θ§FNΘΫ![]() NCΘΫ
NCΘΫ![]() Θ§Φ¥FMΘΫBNΘΫ3Θ§ΗυΨίSΥΡ±Ώ–ΈABCFΘΫSΓςABF+SΓςBFCΘ§Ω…«σΥΡ±Ώ–ΈABCFΒΡΟφΜΐΘΜΘ®3Θ©Ν§Ϋ”AFΘ§ACΘ§ΙΐΒψDΉςDRΓΆAEΘ§”…ΒΎ“ΜΈ ΒΡΫα¬έΚΆ»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟBFΘΫEGΘ§”…SΥΡ±Ώ–ΈAECGΘΫSΓςAEG+SΓςCEGΘΫ
Θ§Φ¥FMΘΫBNΘΫ3Θ§ΗυΨίSΥΡ±Ώ–ΈABCFΘΫSΓςABF+SΓςBFCΘ§Ω…«σΥΡ±Ώ–ΈABCFΒΡΟφΜΐΘΜΘ®3Θ©Ν§Ϋ”AFΘ§ACΘ§ΙΐΒψDΉςDRΓΆAEΘ§”…ΒΎ“ΜΈ ΒΡΫα¬έΚΆ»ΪΒ»»ΐΫ«–ΈΒΡ–‘÷ Ω…ΒΟBFΘΫEGΘ§”…SΥΡ±Ώ–ΈAECGΘΫSΓςAEG+SΓςCEGΘΫ![]() ΓΝEGΓΝAE+
ΓΝEGΓΝAE+![]() ΓΝEGΓΝCFΘΫ
ΓΝEGΓΝCFΘΫ![]() ΓΝBFΓΝAE+
ΓΝBFΓΝAE+![]() ΓΝBFΓΝCFΘΫSΓςABF+SΓςBCFΘΫSΥΡ±Ώ–ΈABCFΘΫSΓςABC+SΓςAFCΘΫ8+SΓςAFCΘ§‘ρΒ±ΒψF‘ΎACΒΡ”“≤ύΘ§«“ΒΫACΨύάκΉν¥σ ±Θ§SΥΡ±Ώ–ΈAECG÷ΒΉν¥σΘ§”…ΒψBΘ§ΒψCΘ§ΒψFΘ§ΒψNΥΡΒψ‘Ύ“‘OΈΣ‘≤–ΡΘ§OCΈΣΑκΨΕΒΡ‘≤…œΘ§Ω…÷ΣΒ±OFΓΆAC ±Θ§ΒψFΒΫACΨύάκΉν¥σΘ§ΗυΨί‘≤ΒΡ”–ΙΊ–‘÷ ΚΆΒ»―ϋ»ΐΫ«–ΈΒΡ–‘÷ Θ§Ω…«σΥΡ±Ώ–ΈAECGΒΡΟφΜΐS «ΒΡΉν¥σ÷ΒΚΆΓœPBCΒΡΕ» ΐΘΜ
ΓΝBFΓΝCFΘΫSΓςABF+SΓςBCFΘΫSΥΡ±Ώ–ΈABCFΘΫSΓςABC+SΓςAFCΘΫ8+SΓςAFCΘ§‘ρΒ±ΒψF‘ΎACΒΡ”“≤ύΘ§«“ΒΫACΨύάκΉν¥σ ±Θ§SΥΡ±Ώ–ΈAECG÷ΒΉν¥σΘ§”…ΒψBΘ§ΒψCΘ§ΒψFΘ§ΒψNΥΡΒψ‘Ύ“‘OΈΣ‘≤–ΡΘ§OCΈΣΑκΨΕΒΡ‘≤…œΘ§Ω…÷ΣΒ±OFΓΆAC ±Θ§ΒψFΒΫACΨύάκΉν¥σΘ§ΗυΨί‘≤ΒΡ”–ΙΊ–‘÷ ΚΆΒ»―ϋ»ΐΫ«–ΈΒΡ–‘÷ Θ§Ω…«σΥΡ±Ώ–ΈAECGΒΡΟφΜΐS «ΒΡΉν¥σ÷ΒΚΆΓœPBCΒΡΕ» ΐΘΜ
ΫβΘΚ
Θ®1Θ©»γΆΦΘ§―”≥ΛAEΫΜBC”ΎΒψQΘ§ΙΐΒψDΉςDRΓΆAEΘ§
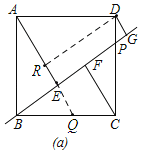
ΓΏΥΡ±Ώ–ΈABCD «’ΐΖΫ–ΈΘ§
ΓύADΘΫBCΘΫ4Θ§ADΓΈBCΘ§
ΓύΓœDARΘΫΓœAQBΘ§
ΓΏΓœAQB+ΓœPBCΘΫ90ΓψΘ§ΓœDAR+ΓœADRΘΫ90ΓψΘ§
ΓύΓœADRΘΫΓœPBCΘ§
ΓΏPCΘΫ3Θ§BCΘΫ4Θ§
ΓύBPΘΫ![]() ΘΫ5Θ§
ΘΫ5Θ§
ΓΏΓœADRΘΫΓœPBCΘ§ΓœARDΘΫΓœBCDΘΫ90ΓψΘ§
ΓύΓςADRΓΉΓςPBCΘ§
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
ΓύDRΘΫ![]() Θ§
Θ§
ÿDRâAEȧDGâBPȧAEâBPȧ
ΓύΥΡ±Ώ–ΈDREG «ΨΊ–ΈΘ§
ΓύEGΘΫDRΘΫ![]() ΘΜ
ΘΜ
Θ®2Θ©»γΆΦΘ§ΙΐΒψFΉςFMΓΆAB”ΎΒψMΘ§ΉςFNΓΆBC”ΎΒψNΘ§
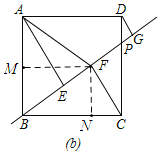
ΓΏΥΡ±Ώ–ΈABCD «’ΐΖΫ–ΈΘ§
ΓύABΘΫBCΘΫ4Θ§ΓœABCΘΫ90ΓψΘ§
ΓΏFMΓΆABΘ§FNΓΆBCΘ§ΓœABCΘΫ90ΓψΘ§
ΓύΥΡ±Ώ–ΈBNFM «ΨΊ–ΈΘ§
ΓύFMΘΫBNΘ§
ΓΏΓœPBCΘΫ30ΓψΘ§
ΓύFCΘΫ![]() BCΘΫ2Θ§ΓœFCBΘΫ60ΓψΘ§
BCΘΫ2Θ§ΓœFCBΘΫ60ΓψΘ§
ΓύΓœNFCΘΫ30ΓψΘ§
ΓύNCΘΫ1Θ§FNΘΫ![]() NCΘΫ
NCΘΫ![]() Θ§
Θ§
ΓύBNΘΫBC©¹NCΘΫ4©¹1ΘΫ3ΘΫMFΘ§
ΓύSΥΡ±Ώ–ΈABCFΘΫSΓςABF+SΓςBFCΘ§
ΓύSΥΡ±Ώ–ΈABCFΘΫ![]() ΓΝ4ΓΝ3+
ΓΝ4ΓΝ3+![]() ΓΝ4ΓΝ
ΓΝ4ΓΝ![]() ΘΫ6+2
ΘΫ6+2![]() ΘΜ
ΘΜ
Θ®3Θ©»γΆΦΘ§Ν§Ϋ”AFΘ§ACΘ§ΙΐΒψDΉςDRΓΆAEΘ§
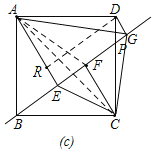
”…ΒΎ“ΜΈ Ω…ΒΟΘ§DRΘΫEGΘ§ΓœADRΘΫΓœPBCΘ§
ΓΏADΘΫBCΘ§ΓœADRΘΫΓœPBCΘ§ΓœARDΘΫΓœCFBΘΫ90ΓψΘ§
ΓύΓςADRΓ’ΓςCBFΘ®AASΘ©
ΓύDRΘΫBFΘ§
ΓύBFΘΫEGΘ§
ΓΏSΥΡ±Ώ–ΈAECGΘΫSΓςAEG+SΓςCEGΘ§
ΓύSΥΡ±Ώ–ΈAECGΘΫ![]() ΓΝEGΓΝAE+
ΓΝEGΓΝAE+![]() ΓΝEGΓΝCFΘΫ
ΓΝEGΓΝCFΘΫ![]() ΓΝBFΓΝAE+
ΓΝBFΓΝAE+![]() ΓΝBFΓΝCFΘΫSΓςABF+SΓςBCFΘ§
ΓΝBFΓΝCFΘΫSΓςABF+SΓςBCFΘ§
ΓύSΥΡ±Ώ–ΈAECGΘΫSΥΡ±Ώ–ΈABCFΘ§
ΓύSΥΡ±Ώ–ΈAECGΘΫSΓςABC+SΓςAFCΘΫ8+SΓςAFCΘ§
ΓύΒ±ΒψF‘ΎACΒΡ”“≤ύΘ§«“ΒΫACΨύάκΉν¥σ ±Θ§SΥΡ±Ώ–ΈAECG÷ΒΉν¥σΘ§
»γΆΦΘ§Ν§Ϋ”BDΫΜAC”ΎΒψNΘ§»ΓBC÷–ΒψOΘ§Ν§Ϋ”ONΘ§OFΫΜAC”ΎΒψMΘ§
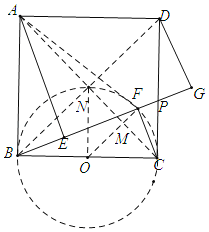
ΓΏΥΡ±Ώ–ΈABCD «’ΐΖΫ–ΈΘ§
ΓύΓœBNCΘΫ90ΓψΘΫΓœBFCΘ§BNΘΫCNΘ§
ΓύΒψBΘ§ΒψCΘ§ΒψFΘ§ΒψNΥΡΒψ‘Ύ“‘OΈΣ‘≤–ΡΘ§OCΈΣΑκΨΕΒΡ‘≤…œΘ§
ΓύOCΘΫOFΘΫONΘΫ2Θ§
ΓΏBNΘΫCNΘ§BOΘΫCOΘ§ΓœBNCΘΫ90ΓψΘ§
ΓύΓœCONΘΫ90ΓψΘ§ΓœBCNΘΫΓœCNOΘΫ45ΓψΘ§
ΓύNCΘΫ![]() Θ§
Θ§
Φ¥ACΘΫ![]() Θ§
Θ§
Β±OFΓΆAC ±Θ§ΒψFΒΫACΒΡΨύάκΉν¥σΘ§
ΓΏOFΓΆACΘ§ONΘΫOCΘ§ΓœNOCΘΫ90ΓψΘ§
ΓύOMΘΫMNΘΫMCΘΫ![]() Θ§ΓœFOCΘΫΓœNOCΘΫ45ΓψΘ§
Θ§ΓœFOCΘΫΓœNOCΘΫ45ΓψΘ§
ΓύFMΘΫ2©¹![]() Θ§
Θ§
ΓύΥΡ±Ώ–ΈAECGΒΡΟφΜΐSΒΡΉν¥σ÷ΒΘΫ8+![]() ΓΝ4
ΓΝ4![]() ΓΝΘ®2©¹
ΓΝΘ®2©¹![]() Θ©ΘΫ4+4
Θ©ΘΫ4+4![]() Θ§
Θ§
ΓΏOBΘΫOFΘ§
ΓύΓœPBOΘΫΓœOFBΘ§
ΓΏΓœPBO+ΓœOFBΘΫΓœFOCΘΫ45ΓψΘ§
ΓύΓœPBCΘΫ22.5ΓψΘ§
ΓύΒ±ΓœPBCΈΣ22.5Γψ ±Θ§S”–Ήν¥σ÷ΒΘ§Ήν¥σ÷Β «4+4![]() .
.

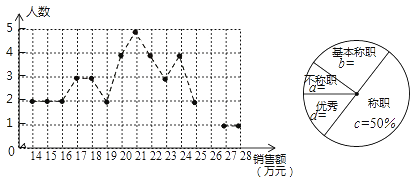
ΓΨΧβΡΩΓΩ―τΙβ –≥ΓΡ≥ΗωΧε…ΧΜßΙΚΫχΡ≥÷÷ΒγΉ”≤ζΤΖΘ§ΟΩΗωΫχΦέ50‘ΣΘ°Βς≤ιΖΔœ÷Θ§Β± έΦέΈΣ80‘Σ ±Θ§ΤΫΨυ“Μ÷ήΩ…¬τ≥ω160ΗωΘ§ΕχΒ±ΟΩ έΦέΟΩΫΒΒΆ2‘Σ ±Θ§ΤΫΨυ“Μ÷ήΩ…Εύ¬τ≥ω20ΗωΘ°»τ…ηΟΩΗωΒγΉ”≤ζΤΖΫΒΦέx‘ΣΘ§
Θ®1Θ©ΗυΨίΧβ“βΘ§Χν±μΘΚ
ΫχΦέΘ®‘ΣΘ© | έΦέΘ®‘ΣΘ© | ΟΩΦΰάϊ»σΘ®‘ΣΘ© | œζΝΩΘ®ΗωΘ© | Ήήάϊ»σΘ®‘ΣΘ© | |
ΫΒΦέ«Α | 50 | 80 | 30 | 160 |
|
ΫΒΦέΚσ | 50 | ________ | ________ | ________ | ________ |
Θ®2Θ©»τ…ΧΜßΦΤΜ°ΟΩ÷ή”·άϊ5200‘ΣΘ§«“ΨΓΝΩΦθ…ΌΩβ¥φΘ§‘ρΟΩΗωΒγΉ”≤ζΤΖ”ΠΫΒΦέΕύ…Ό‘ΣΘΩ