题目内容
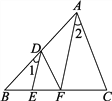
【题目】如图，已知AF平分∠BAC，DE平分∠BDF，且∠1=∠2.
(1)DF∥AC吗，为什么？
(2)DE与AF的位置关系又如何？
【答案】试题见解析
【解析】分析：（1）根据角平分线的性质可得∠2=
∠BAC，∠1=∠BDF，再有∠1=∠2，可得∠BDF=∠BAC，根据同位角相等，两直线平行即可证得结论；
（2）先根据DF∥AC可得∠2=∠BAF，再有∠1=∠2可得∠1=∠BAF，根据内错角相等，两直线平行即可证得结论.
解：(1)因为AF平分∠BAC，DE平分∠BDF，所以∠2=∠BAC，∠1=∠BDF，又因为∠1=∠2，所以∠BDF=∠BAC，所以DF∥AC；
(2)DE∥AF.理由如下：因为AF平分∠BAC，所以∠2=∠BAF，又因为∠1=∠2，所以∠1=∠BAF，所以DE∥AF.
练习册系列答案
阅读快车系列答案
相关题目
