题目内容
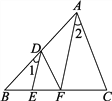
【题目】如图,ABCD对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF. 
(1)根据题意,补全图形;
(2)求证:BE=DF.
【答案】
(1)解:图象如图所示.

(2)证明:∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵E,F分别是OA,OC的中点,
∴OE= ![]() OA,OF=
OA,OF= ![]() OC,
OC,
∴OE=OF,
在△BOE和△DOF中,
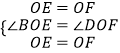 ,
,
∴△BOE≌△DOF(SAS),
∴BE=DF
【解析】(1)根据要求画出图象即可.(2)只要证明△BOE≌△DOF(SAS),即可解决问题.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分).

练习册系列答案
相关题目