题目内容
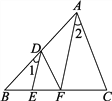
【题目】如图一:在Rt△ABC中,∠C=90°AD、BE分别是△ABC中∠A、∠B的平分线,AD、BE交于点F,过F点做FH⊥AD交AC于点H,易证:AH+DB=AB;
(1)若将Rt△ABC中∠BAC、∠ABC的内角平分线改成外角平分线,即:AF、BF分别是∠BAC、∠ABC的外角平分线交于F点,FH⊥AF交直线AC于H点,如图二:请写出线段AH、BD、AB之间的数量关系,并证明。
(2)若将Rt△ABC中∠BAC、∠ABC的内角平分线改成一个是外角平分线,即:AF是∠A的内角平分线,BE是∠B的外角平分线交于F点,FH⊥AD交AC于点H.如图三:请写出线段AH、BD、AB之间的数量关系,无需证明。
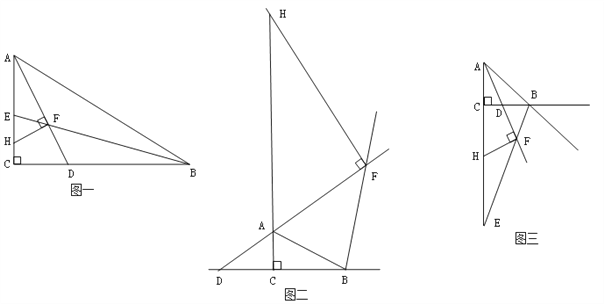
【答案】(1) AH=AB+BD ,证明见解析;(2) AH=AB+BD
【解析】(1)的结论是:AH=AB+BD
(2)的结论是:AH=AB+BD
(1)的结论证明如下:
∵AF平分∠BAH
∴∠BAF=∠HAF
∵AF⊥HM
∴△HAF≌△MAF
∴AH=AM ∠AHF=∠M
∵AF平分∠BAH
∴∠ABF=∠FBN
∵∠AHF+∠HAF=90°
∵∠DAC+∠ADB=90°
∴∠ADB=∠AHF
∴∠FDB=∠BMF
∴△DFB≌△MFB
∴DB=BM
∵AM=AB+BM
∴AH=AB+DB

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
【题目】八(2)班组织了一次经典朗读比赛,甲、乙两队各10人的比赛成绩如表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是分,乙队成绩的众数是分;
(2)计算甲、乙队的平均成绩和方差,试说明成绩较为整齐的是哪一队?