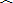题目内容
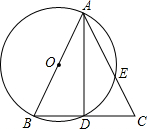
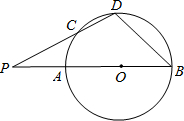
如图,P为⊙O外一点,过点P作⊙O的两条割线,分别交⊙O于A、B和C、D,且AB为⊙O的直径,已知PA=AO=2cm,弧AC=弧CD,则PC的长为( )
| A.4cm | B.2
| C.
| D.2
|

连接OC、OD.
∵弧AC=弧CD,
∴∠AOC=COD=
∠AOD;
又∵∠ABD=
∠AOD,
∴∠ABD=∠AOC,
∴OC∥BD,
∴
=
,
∴
=
=
,
∴PD=
PC;
∵PD和PB都是⊙O外同一点引出的割线,
∴PC•PD=PA•PB,
∴PC•PD=2×6=12,
∴PC=2
cm.
故选D.
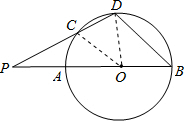
∵弧AC=弧CD,
∴∠AOC=COD=
| 1 |
| 2 |
又∵∠ABD=
| 1 |
| 2 |
∴∠ABD=∠AOC,
∴OC∥BD,
∴
| PC |
| PD |
| PO |
| PB |
∴
| PC |
| PD |
| 4 |
| 6 |
| 2 |
| 3 |
∴PD=
| 3 |
| 2 |
∵PD和PB都是⊙O外同一点引出的割线,
∴PC•PD=PA•PB,
∴PC•PD=2×6=12,
∴PC=2
| 2 |
故选D.


练习册系列答案
相关题目