题目内容
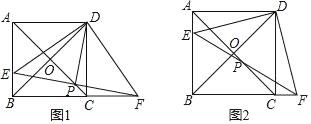
【题目】如图1,在正方形ABCD中,对角线AC,BD交于点O,点E在AB上,点F在BC的延长线上,且AE=CF,连接EF交AC于点P,分别连接DE,DF,DP.
(1)求证:△ADE≌△CDF;
(2)求证:△ADP∽△BDF;
(3)如图2,若PE=BE,则![]() 的值是 (直按写出结果即可).
的值是 (直按写出结果即可).
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
(1)根据SAS证明即可.
(2)想办法证明∠DAP=∠DBF,∠ADP=∠BDF即可解决问题.
(3)如图2中,作PH⊥BC于H.首先证明∠EFB=30°,设HP=HC=m,则PC=![]() m,HF=
m,HF=![]() m,求出CF即可解决问题.
m,求出CF即可解决问题.
(1)∵四边形ABCD是正方形,
∴DA=DC,∠DAE=∠BCD=∠DCF=90°,
∵AE=CF,
∴△ADE≌△CDF(SAS).
(2)作FH∥AB交AC的延长线于H.
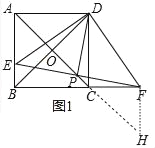
∵四边形ABCD是正方形,
∴∠ACB=∠FCH=45°,
∵AB∥FH,
∴∠HFC=∠ABC=90°,
∴∠FCH=∠H=45°,
∴CF=FH=AE,
∵∠PAE=∠H,∠APE=∠FPH,
∴△APE≌△HPF(AAS),
∴PE=PF,
∵△ADE≌△CDF,
∴DE=DF,∠ADE=∠CDF,∠ADE=∠CDF,
∴∠EFD=∠ADC=90°,
∴△DEF是等腰直角三角形,
∵EP=PF,
∴∠EDP=∠FDP=45°,
∵ADP=∠ADE+∠PDE=∠ADE+45°,∠BDP=∠CDF+∠BDC=∠CDF+45°,
∴∠ADP=∠BDF,
∵∠DAP=∠DBF=45°,
∴△ADP∽△BDF.
(3)如图2中,作PH⊥BC于H.
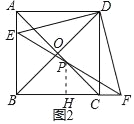
由(2)可知:PE=PF,
∵BE=PE,
∴EF=2BE,
∵∠EBF=90°,
∴sin∠EFB=![]() ,
,
∴∠EFB=30°,
∵PH⊥FH,∠PCH=45°,
∴∠PHC=90°,∠HPC=∠HCP=45°,
∴HP=HC,设HP=HC=m,则![]()
∴CF=![]() m﹣m,
m﹣m,
∴![]()
故答案为: ![]()

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案