Question

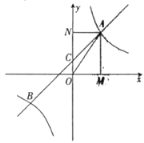
【题目】已知，如图，数轴上有A、B两点．

（1）线段AB的中点表示的数是　 　；

（2）线段AB的长度是　 　；

（3）若A、B两点问时向右运动，A点速度是每秒3个单位长度，B点速度是每秒2个单位长度，问经过几秒时AB＝2？

Answer 1

【答案】（1）（2）5（3）经过3秒或7秒时，线段AB的长度为2

【解析】

（1）线段AB的中点对应的数为两端点对应的数的和的一半；

（2）线段AB的长度是两端点对应的数的差的绝对值；

（3）两个不同动点相距2个单位长度，两种情况：一是相遇前相距2单位长度，二是相遇后相距2个单位长度，最后根据路，速度和时间的关系建立等量关系．

如图所示：

（1）∵有A、B两点在数轴上对应的数分别为﹣2，3

∴线段AB的中点表示的数是；

故答案为：；

（2）线段AB的长度是|﹣2﹣3|＝|﹣5|＝5，

故答案为：5；

（3）设经过x秒后，线段AB的长度为2，依题意得：

①A点还没有追上B点某一时刻相距2个单位长度时，

5+2x＝3x+2，

解得：x＝3，；

②A点追上B点后某一时刻相距2个单位长度时，

3x＝2x+5+2，

解得：x＝7；

综合所述经过3秒或7秒时，线段AB的长度为2．