题目内容
【题目】如图,在![]() 中,
中,![]() ,
,![]() 、
、![]() 是斜边
是斜边![]() 上两点,且
上两点,且![]() ,将
,将![]() 绕
绕![]() 顺时针旋转
顺时针旋转![]() 后,得到
后,得到![]() ,连接
,连接![]() ,则下列结论不正确的是( )
,则下列结论不正确的是( )
A.![]() B.
B.![]() 为等腰直角三角形
为等腰直角三角形
C.![]() 平分
平分![]() D.
D.![]()
【答案】B
【解析】
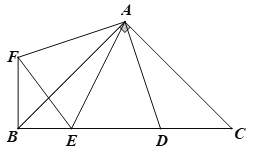
由已知![]() 和旋转的性质可判断A项,进一步可判断C项;利用SAS可证明△AED≌△AEF,可得ED=EF,容易证明△FBE是直角三角形,由此可判断D项和B项,于是可得答案.
和旋转的性质可判断A项,进一步可判断C项;利用SAS可证明△AED≌△AEF,可得ED=EF,容易证明△FBE是直角三角形,由此可判断D项和B项,于是可得答案.
解:∵△ADC绕点A顺时针旋转90°得△AFB,
∴△ADC≌△AFB,∠FAD=90°,AD=AF,
∵∠DAE=45°,
∴∠FAE=90°-∠DAE=45°,所以A正确;
∴∠DAE=∠FAE,
∴![]() 平分
平分![]() ,所以C正确;
,所以C正确;
∵
∴△AED≌△AEF(SAS),
∴ED=EF,
在Rt△ABC中,∠ABC+∠C=90°,
又∵∠C=∠ABF,
∴∠ABC+∠ABF=90°,即∠FBE=90°,
∴在Rt△FBE中,由勾股定理得:![]() ,
,
∴![]() ,所以D正确;
,所以D正确;
而BE、CD不一定相等,所以BE、BF不一定相等,所以B不正确.
故选B.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】二次函数![]() (a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | … | -1 | 0 | 1 | 3 | … |
y | … | -3 | 1 | 3 | 1 | … |
则下列判断中正确的是( )
A.抛物线开口向上B.抛物线与y轴交于负半轴
C.抛物线的顶点为(1,3)D.一元二次方程ax2+bx+c=0的正根在3与4之间