题目内容
【题目】阅读下面材料:
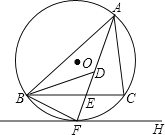
小红遇到这样一个问题:如图1,在四边形ABCD中,∠A=∠C=90°,∠D=60°,AB=![]() ,BC=
,BC=![]() ,求AD的长.
,求AD的长.
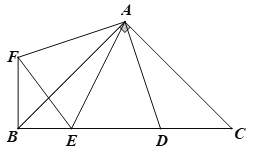
小红发现,延长AB与DC相交于点E,通过构造Rt△ADE,经过推理和计算能够使问题得到解决(如图2).
请回答:AD的长为 .
参考小红思考问题的方法,解决问题:
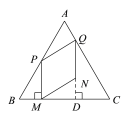
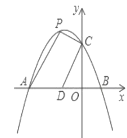
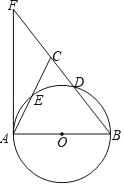
如图3,在四边形ABCD中,tanA=![]() ,∠B=∠C=135°,AB=9,CD=3,求BC和AD的长.
,∠B=∠C=135°,AB=9,CD=3,求BC和AD的长.

【答案】(1)6;(2)BC=![]() ,AD=
,AD=![]() .
.
【解析】
(1)延长AB与DC相交于点E,解直角三角形BEC,得出BE的长,那么AE=AB+BE,再解直角三角形ADE,即可求出AD;
(2)延长AB与DC相交于点E.由∠ABC=∠BCD=135°,得出∠EBC=∠ECB=45°,那么BE=CE,∠E=90°.设BE=CE=x,则BC=![]() x,AE=9+x,DE=3+x.在Rt△ADE中,由tanA=
x,AE=9+x,DE=3+x.在Rt△ADE中,由tanA=![]() ,得出
,得出![]() ,求出x=3,那么BC=3
,求出x=3,那么BC=3![]() ,AE=12,DE=6,再利用勾股定理即可求出AD.
,AE=12,DE=6,再利用勾股定理即可求出AD.
(1)如图,延长AB与DC相交于点E,
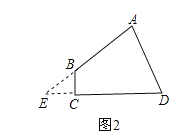
在△ADE中,
∵∠A=90°,∠D=60°,
∴∠E=30°.
在Rt△BEC中,
∵∠BCE=90°,∠E=30°,BC=![]() ,
,
∴BE=2BC=2![]() ,
,
∴AE=AB+BE=4![]() +2
+2![]() =6
=6![]() .
.
在Rt△ADE中,
∵∠A=90°,∠E=30°,AE=6![]() ,
,
∴AD=AEtan∠E=6![]() ×
×![]() =6.
=6.
故答案为:6;
(2)如图,延长AB与DC相交于点E.
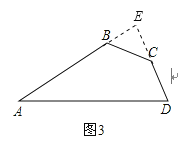
∵∠ABC=∠BCD=135°,
∴∠EBC=∠ECB=45°,
∴BE=CE,∠E=90°.
设BE=CE=x,则BC=![]() x,AE=9+x,DE=3+x.
x,AE=9+x,DE=3+x.
在Rt△ADE中,∠E=90°.
∵tanA=![]() ,
,
∴![]() ,即
,即![]() ,
,
∴x=3.
经检验x=3是所列方程的解,且符合题意,
∴BC=3![]() ,AE=12,DE=6,
,AE=12,DE=6,
∴AD=![]() =6
=6![]() .
.

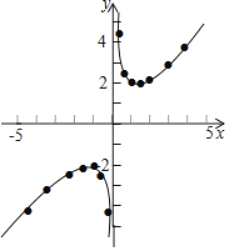
【题目】已知关于x的函数y=![]() +x,如表是y与x的几组对应值:
+x,如表是y与x的几组对应值:
x | … | ﹣4 | ﹣3 | -2 | - | -1 | - | - |
|
| 1 |
| 2 | 3 | 4 | … |
y | … | - | - | - | - | -2 | - | - |
|
| 2 |
|
|
|
| … |
如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点画出了此函数的图象请你根据学习函数的经验,根据画出的函数图象特征,对该函数的图象与性质进行探究:
(1)该函数的图象关于 对称;
(2)在y轴右侧,函数变化规律是当0<x<1,y随x的增大而减小;当x>1,y随x的增大而增大.在y轴左侧,函数变化规律是 .
(3)函数y=![]() 当x 时,y有最 值为 .
当x 时,y有最 值为 .
(4)若方程![]() +x=m有两个不相等的实数根,则m的取值范围是 .
+x=m有两个不相等的实数根,则m的取值范围是 .