题目内容
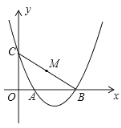
【题目】如图，抛物线
交x轴于点A，B，交y轴于点C，当
纸片上的C沿着此抛物线运动时，则纸片随之也跟着水平移动，设纸片上CB的中点M坐标为
，在此运动过程中，n与m的关系式是（ ）
A.
B.
C.
D.
【答案】D
【解析】
先分别求出平移前B、C、M的坐标，从而得出：点M可以向左平移2个单位，再向上平行1个单位得到点C，再根据平移后C和M的相对位置不变，从而用m、n表示出点C坐标，代入解析式中即可求出n与m的关系式.
解：平移前：
将y=0代入
中，得
解得：
∴由图可知：点A坐标为（1,0），点B的坐标为（4,0）
将x=0代入中，得y=2
∴点C的坐标为（0,2）
∴此时BC的中点M的坐标为
此时点M可以向左平移2个单位，再向上平行1个单位得到点C
平移后：
∵C和M的相对位置不变
∴此时点M可以向左平移2个单位，再向上平行1个单位得到点C
∵纸片上CB的中点M坐标为
，
∴点C的坐标为（m－2,n＋1）
将点C坐标代入中，得
整理得：
配方得：
故选D.
【题目】已知关于x的函数y＝
+x，如表是y与x的几组对应值：
x | … | ﹣4 | ﹣3 | -2 | - | -1 | - | - |
|
| 1 |
| 2 | 3 | 4 | … |
y | … | - | - | - | - | -2 | - | - |
|
| 2 |
|
|
|
| … |
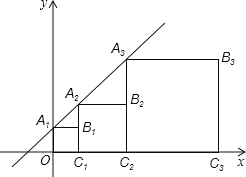
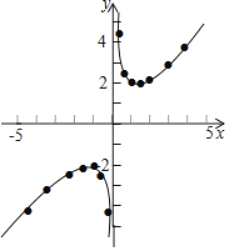
如图，在平面直角坐标系xOy中，描出了以上表中各对对应值为坐标的点，根据描出的点画出了此函数的图象请你根据学习函数的经验，根据画出的函数图象特征，对该函数的图象与性质进行探究：
（1）该函数的图象关于 对称；
（2）在y轴右侧，函数变化规律是当0＜x＜1，y随x的增大而减小；当x＞1，y随x的增大而增大．在y轴左侧，函数变化规律是 ．
（3）函数y＝
当x 时，y有最 值为 ．
（4）若方程+x＝m有两个不相等的实数根，则m的取值范围是 ．
【题目】为了丰富同学们的知识，拓展阅读视野，学习图书馆购买了一些科技、文学、历史等书籍，进行组合搭配成
、
、
三种套型书籍，发放给各班级的图书角供同学们阅读，已知各套型的规格与价格如下表：
|
|
| |
规格（本/套） | 12 | 9 | 7 |
价格（元/套） | 200 | 150 | 120 |
（1）已知搭配、两种套型书籍共15套，需购买书籍的花费是2120元，问、两种套型各多少套？
（2）若图书馆用来搭配的书籍共有2100本，现将其搭配成、两种套型书籍，这两种套型的总价为30750元，求搭配后剩余多少本书？
（3）若图书馆用来搭配的书籍共有122本，现将其搭配成、、三种套型书籍共13套，且没有剩余，请求出所有搭配的方案．
